Mass
| Mass | |
|---|---|
 A 2 kg (4.4 lb) cast iron weight used for balances | |
Common symbols | m |
| SI unit | kilogram |
| Extensive? | yes |
| Conserved? | yes |
| Part of a series on |
| Classical mechanics |
|---|
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration (change of velocity) when a net force is applied.[1] The object's mass also determines the strength of its gravitational attraction to other bodies.
The SI base unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh less than it does on Earth because of the lower gravity, but it would still have the same mass. This is because weight is a force, while mass is the property that (along with gravity) determines the strength of this force.
In the Standard Model of physics, the mass of elementary particles is believed to be a result of their coupling with the Higgs boson in what is known as the Brout–Englert–Higgs mechanism.[2]
Phenomena
There are several distinct phenomena that can be used to measure mass. Although some theorists have speculated that some of these phenomena could be independent of each other,[3] current experiments have found no difference in results regardless of how it is measured:
- Inertial mass measures an object's resistance to being accelerated by a force (represented by the relationship F = ma).
- Active gravitational mass determines the strength of the gravitational field generated by an object.
- Passive gravitational mass measures the gravitational force exerted on an object in a known gravitational field.
The mass of an object determines its acceleration in the presence of an applied force. The inertia and the inertial mass describe this property of physical bodies at the qualitative and quantitative level respectively. According to Newton's second law of motion, if a body of fixed mass m is subjected to a single force F, its acceleration a is given by F/m. A body's mass also determines the degree to which it generates and is affected by a gravitational field. If a first body of mass mA is placed at a distance r (center of mass to center of mass) from a second body of mass mB, each body is subject to an attractive force Fg = GmAmB/r2, where G = 6.67×10−11 N⋅kg−2⋅m2 is the "universal gravitational constant". This is sometimes referred to as gravitational mass.[note 1] Repeated experiments since the 17th century have demonstrated that inertial and gravitational mass are identical; since 1915, this observation has been incorporated a priori in the equivalence principle of general relativity.
Units of mass

The International System of Units (SI) unit of mass is the kilogram (kg). The kilogram is 1000 grams (g), and was first defined in 1795 as the mass of one cubic decimetre of water at the melting point of ice. However, because precise measurement of a cubic decimetre of water at the specified temperature and pressure was difficult, in 1889 the kilogram was redefined as the mass of a metal object, and thus became independent of the metre and the properties of water, this being a copper prototype of the grave in 1793, the platinum Kilogramme des Archives in 1799, and the platinum–iridium International Prototype of the Kilogram (IPK) in 1889.
However, the mass of the IPK and its national copies have been found to drift over time. The re-definition of the kilogram and several other units came into effect on 20 May 2019, following a final vote by the CGPM in November 2018.[4] The new definition uses only invariant quantities of nature: the speed of light, the caesium hyperfine frequency, the Planck constant and the elementary charge.[5]
Non-SI units accepted for use with SI units include:
- the tonne (t) (or "metric ton"), equal to 1000 kg
- the electronvolt (eV), a unit of energy, used to express mass in units of eV/c2 through mass–energy equivalence
- the dalton (Da), equal to 1/12 of the mass of a free carbon-12 atom, approximately 1.66×10−27 kg.[note 2]
Outside the SI system, other units of mass include:
- the slug (sl), an Imperial unit of mass (about 14.6 kg)
- the pound (lb), a unit of mass (about 0.45 kg), which is used alongside the similarly named pound (force) (about 4.5 N), a unit of force[note 3]
- the Planck mass (about 2.18×10−8 kg), a quantity derived from fundamental constants
- the solar mass (M☉), defined as the mass of the Sun, primarily used in astronomy to compare large masses such as stars or galaxies (≈ 1.99×1030 kg)
- the mass of a particle, as identified with its inverse Compton wavelength (1 cm−1 ≘ 3.52×10−41 kg)
- the mass of a star or black hole, as identified with its Schwarzschild radius (1 cm ≘ 6.73×1024 kg).
Definitions
In physical science, one may distinguish conceptually between at least seven different aspects of mass, or seven physical notions that involve the concept of mass.[6] Every experiment to date has shown these seven values to be proportional, and in some cases equal, and this proportionality gives rise to the abstract concept of mass. There are a number of ways mass can be measured or operationally defined:
- Inertial mass is a measure of an object's resistance to acceleration when a force is applied. It is determined by applying a force to an object and measuring the acceleration that results from that force. An object with small inertial mass will accelerate more than an object with large inertial mass when acted upon by the same force. One says the body of greater mass has greater inertia.
- Active gravitational mass[note 4] is a measure of the strength of an object's gravitational flux (gravitational flux is equal to the surface integral of gravitational field over an enclosing surface). Gravitational field can be measured by allowing a small "test object" to fall freely and measuring its free-fall acceleration. For example, an object in free-fall near the Moon is subject to a smaller gravitational field, and hence accelerates more slowly, than the same object would if it were in free-fall near the Earth. The gravitational field near the Moon is weaker because the Moon has less active gravitational mass.
- Passive gravitational mass is a measure of the strength of an object's interaction with a gravitational field. Passive gravitational mass is determined by dividing an object's weight by its free-fall acceleration. Two objects within the same gravitational field will experience the same acceleration; however, the object with a smaller passive gravitational mass will experience a smaller force (less weight) than the object with a larger passive gravitational mass.
- According to relativity, mass is nothing else than the rest energy of a system of particles, meaning the energy of that system in a reference frame where it has zero momentum. Mass can be converted into other forms of energy according to the principle of mass–energy equivalence. This equivalence is exemplified in a large number of physical processes including pair production, beta decay and nuclear fusion. Pair production and nuclear fusion are processes in which measurable amounts of mass are converted to kinetic energy or vice versa.
- Curvature of spacetime is a relativistic manifestation of the existence of mass. Such curvature is extremely weak and difficult to measure. For this reason, curvature was not discovered until after it was predicted by Einstein's theory of general relativity. Extremely precise atomic clocks on the surface of the Earth, for example, are found to measure less time (run slower) when compared to similar clocks in space. This difference in elapsed time is a form of curvature called gravitational time dilation. Other forms of curvature have been measured using the Gravity Probe B satellite.
- Quantum mass manifests itself as a difference between an object's quantum frequency and its wave number. The quantum mass of a particle is proportional to the inverse Compton wavelength and can be determined through various forms of spectroscopy. In relativistic quantum mechanics, mass is one of the irreducible representation labels of the Poincaré group.
Weight vs. mass

In everyday usage, mass and "weight" are often used interchangeably. For instance, a person's weight may be stated as 75 kg. In a constant gravitational field, the weight of an object is proportional to its mass, and it is unproblematic to use the same unit for both concepts. But because of slight differences in the strength of the Earth's gravitational field at different places, the distinction becomes important for measurements with a precision better than a few percent, and for places far from the surface of the Earth, such as in space or on other planets. Conceptually, "mass" (measured in kilograms) refers to an intrinsic property of an object, whereas "weight" (measured in newtons) measures an object's resistance to deviating from its current course of free fall, which can be influenced by the nearby gravitational field. No matter how strong the gravitational field, objects in free fall are weightless, though they still have mass.[7]
The force known as "weight" is proportional to mass and acceleration in all situations where the mass is accelerated away from free fall. For example, when a body is at rest in a gravitational field (rather than in free fall), it must be accelerated by a force from a scale or the surface of a planetary body such as the Earth or the Moon. This force keeps the object from going into free fall. Weight is the opposing force in such circumstances and is thus determined by the acceleration of free fall. On the surface of the Earth, for example, an object with a mass of 50 kilograms weighs 491 newtons, which means that 491 newtons is being applied to keep the object from going into free fall. By contrast, on the surface of the Moon, the same object still has a mass of 50 kilograms but weighs only 81.5 newtons, because only 81.5 newtons is required to keep this object from going into a free fall on the moon. Restated in mathematical terms, on the surface of the Earth, the weight W of an object is related to its mass m by W = mg, where g = 9.80665 m/s2 is the acceleration due to Earth's gravitational field, (expressed as the acceleration experienced by a free-falling object).
For other situations, such as when objects are subjected to mechanical accelerations from forces other than the resistance of a planetary surface, the weight force is proportional to the mass of an object multiplied by the total acceleration away from free fall, which is called the proper acceleration. Through such mechanisms, objects in elevators, vehicles, centrifuges, and the like, may experience weight forces many times those caused by resistance to the effects of gravity on objects, resulting from planetary surfaces. In such cases, the generalized equation for weight W of an object is related to its mass m by the equation W = –ma, where a is the proper acceleration of the object caused by all influences other than gravity. (Again, if gravity is the only influence, such as occurs when an object falls freely, its weight will be zero).
Inertial vs. gravitational mass
Although inertial mass, passive gravitational mass and active gravitational mass are conceptually distinct, no experiment has ever unambiguously demonstrated any difference between them. In classical mechanics, Newton's third law implies that active and passive gravitational mass must always be identical (or at least proportional), but the classical theory offers no compelling reason why the gravitational mass has to equal the inertial mass. That it does is merely an empirical fact.
Albert Einstein developed his general theory of relativity starting with the assumption that the inertial and passive gravitational masses are the same. This is known as the equivalence principle.
The particular equivalence often referred to as the "Galilean equivalence principle" or the "weak equivalence principle" has the most important consequence for freely falling objects. Suppose an object has inertial and gravitational masses m and M, respectively. If the only force acting on the object comes from a gravitational field g, the force on the object is:
Given this force, the acceleration of the object can be determined by Newton's second law:
Putting these together, the gravitational acceleration is given by:
This says that the ratio of gravitational to inertial mass of any object is equal to some constant K if and only if all objects fall at the same rate in a given gravitational field. This phenomenon is referred to as the "universality of free-fall". In addition, the constant K can be taken as 1 by defining our units appropriately.
The first experiments demonstrating the universality of free-fall were—according to scientific 'folklore'—conducted by Galileo obtained by dropping objects from the Leaning Tower of Pisa. This is most likely apocryphal: he is more likely to have performed his experiments with balls rolling down nearly frictionless inclined planes to slow the motion and increase the timing accuracy. Increasingly precise experiments have been performed, such as those performed by Loránd Eötvös,[8] using the torsion balance pendulum, in 1889. As of 2008[update], no deviation from universality, and thus from Galilean equivalence, has ever been found, at least to the precision 10−6. More precise experimental efforts are still being carried out.[9]
The universality of free-fall only applies to systems in which gravity is the only acting force. All other forces, especially friction and air resistance, must be absent or at least negligible. For example, if a hammer and a feather are dropped from the same height through the air on Earth, the feather will take much longer to reach the ground; the feather is not really in free-fall because the force of air resistance upwards against the feather is comparable to the downward force of gravity. On the other hand, if the experiment is performed in a vacuum, in which there is no air resistance, the hammer and the feather should hit the ground at exactly the same time (assuming the acceleration of both objects towards each other, and of the ground towards both objects, for its own part, is negligible). This can easily be done in a high school laboratory by dropping the objects in transparent tubes that have the air removed with a vacuum pump. It is even more dramatic when done in an environment that naturally has a vacuum, as David Scott did on the surface of the Moon during Apollo 15.
A stronger version of the equivalence principle, known as the Einstein equivalence principle or the strong equivalence principle, lies at the heart of the general theory of relativity. Einstein's equivalence principle states that within sufficiently small regions of spacetime, it is impossible to distinguish between a uniform acceleration and a uniform gravitational field. Thus, the theory postulates that the force acting on a massive object caused by a gravitational field is a result of the object's tendency to move in a straight line (in other words its inertia) and should therefore be a function of its inertial mass and the strength of the gravitational field.
Origin
In theoretical physics, a mass generation mechanism is a theory which attempts to explain the origin of mass from the most fundamental laws of physics. To date, a number of different models have been proposed which advocate different views of the origin of mass. The problem is complicated by the fact that the notion of mass is strongly related to the gravitational interaction but a theory of the latter has not been yet reconciled with the currently popular model of particle physics, known as the Standard Model.
Pre-Newtonian concepts
Weight as an amount

The concept of amount is very old and predates recorded history. The concept of "weight" would incorporate "amount" and acquire a double meaning that was not clearly recognized as such.[10]
What we now know as mass was until the time of Newton called “weight.” ... A goldsmith believed that an ounce of gold was a quantity of gold. ... But the ancients believed that a beam balance also measured “heaviness” which they recognized through their muscular senses. ... Mass and its associated downward force were believed to be the same thing.
— K. M. Browne, The pre-Newtonian meaning of the word “weight”
Humans, at some early era, realized that the weight of a collection of similar objects was directly proportional to the number of objects in the collection:
where W is the weight of the collection of similar objects and n is the number of objects in the collection. Proportionality, by definition, implies that two values have a constant ratio:
- , or equivalently
An early use of this relationship is a balance scale, which balances the force of one object's weight against the force of another object's weight. The two sides of a balance scale are close enough that the objects experience similar gravitational fields. Hence, if they have similar masses then their weights will also be similar. This allows the scale, by comparing weights, to also compare masses.
Consequently, historical weight standards were often defined in terms of amounts. The Romans, for example, used the carob seed (carat or siliqua) as a measurement standard. If an object's weight was equivalent to 1728 carob seeds, then the object was said to weigh one Roman pound. If, on the other hand, the object's weight was equivalent to 144 carob seeds then the object was said to weigh one Roman ounce (uncia). The Roman pound and ounce were both defined in terms of different sized collections of the same common mass standard, the carob seed. The ratio of a Roman ounce (144 carob seeds) to a Roman pound (1728 carob seeds) was:
Planetary motion
In 1600 AD, Johannes Kepler sought employment with Tycho Brahe, who had some of the most precise astronomical data available. Using Brahe's precise observations of the planet Mars, Kepler spent the next five years developing his own method for characterizing planetary motion. In 1609, Johannes Kepler published his three laws of planetary motion, explaining how the planets orbit the Sun. In Kepler's final planetary model, he described planetary orbits as following elliptical paths with the Sun at a focal point of the ellipse. Kepler discovered that the square of the orbital period of each planet is directly proportional to the cube of the semi-major axis of its orbit, or equivalently, that the ratio of these two values is constant for all planets in the Solar System.[note 5]
On 25 August 1609, Galileo Galilei demonstrated his first telescope to a group of Venetian merchants, and in early January 1610, Galileo observed four dim objects near Jupiter, which he mistook for stars. However, after a few days of observation, Galileo realized that these "stars" were in fact orbiting Jupiter. These four objects (later named the Galilean moons in honor of their discoverer) were the first celestial bodies observed to orbit something other than the Earth or Sun. Galileo continued to observe these moons over the next eighteen months, and by the middle of 1611, he had obtained remarkably accurate estimates for their periods.
Galilean free fall


Sometime prior to 1638, Galileo turned his attention to the phenomenon of objects in free fall, attempting to characterize these motions. Galileo was not the first to investigate Earth's gravitational field, nor was he the first to accurately describe its fundamental characteristics. However, Galileo's reliance on scientific experimentation to establish physical principles would have a profound effect on future generations of scientists. It is unclear if these were just hypothetical experiments used to illustrate a concept, or if they were real experiments performed by Galileo,[11] but the results obtained from these experiments were both realistic and compelling. A biography by Galileo's pupil Vincenzo Viviani stated that Galileo had dropped balls of the same material, but different masses, from the Leaning Tower of Pisa to demonstrate that their time of descent was independent of their mass.[note 6] In support of this conclusion, Galileo had advanced the following theoretical argument: He asked if two bodies of different masses and different rates of fall are tied by a string, does the combined system fall faster because it is now more massive, or does the lighter body in its slower fall hold back the heavier body? The only convincing resolution to this question is that all bodies must fall at the same rate.[12]
A later experiment was described in Galileo's Two New Sciences published in 1638. One of Galileo's fictional characters, Salviati, describes an experiment using a bronze ball and a wooden ramp. The wooden ramp was "12 cubits long, half a cubit wide and three finger-breadths thick" with a straight, smooth, polished groove. The groove was lined with "parchment, also smooth and polished as possible". And into this groove was placed "a hard, smooth and very round bronze ball". The ramp was inclined at various angles to slow the acceleration enough so that the elapsed time could be measured. The ball was allowed to roll a known distance down the ramp, and the time taken for the ball to move the known distance was measured. The time was measured using a water clock described as follows:
- a large vessel of water placed in an elevated position; to the bottom of this vessel was soldered a pipe of small diameter giving a thin jet of water, which we collected in a small glass during the time of each descent, whether for the whole length of the channel or for a part of its length; the water thus collected was weighed, after each descent, on a very accurate balance; the differences and ratios of these weights gave us the differences and ratios of the times, and this with such accuracy that although the operation was repeated many, many times, there was no appreciable discrepancy in the results.[13]
Galileo found that for an object in free fall, the distance that the object has fallen is always proportional to the square of the elapsed time:
Galileo had shown that objects in free fall under the influence of the Earth's gravitational field have a constant acceleration, and Galileo's contemporary, Johannes Kepler, had shown that the planets follow elliptical paths under the influence of the Sun's gravitational mass. However, Galileo's free fall motions and Kepler's planetary motions remained distinct during Galileo's lifetime.
Mass as distinct from weight
According to K. M. Browne: "Kepler formed a [distinct] concept of mass ('amount of matter' (copia materiae)), but called it 'weight' as did everyone at that time."[10] Finally, in 1686, Newton gave this distinct concept its own name. In the first paragraph of Principia, Newton defined quantity of matter as “density and bulk conjunctly”, and mass as quantity of matter.[14]
The quantity of matter is the measure of the same, arising from its density and bulk conjunctly. ... It is this quantity that I mean hereafter everywhere under the name of body or mass. And the same is known by the weight of each body; for it is proportional to the weight.
— Isaac Newton, Mathematical principles of natural philosophy, Definition I.
Newtonian mass
| Earth's Moon | Mass of Earth | |
|---|---|---|
| Semi-major axis | Sidereal orbital period | |
| 0.002 569 AU | 0.074 802 sidereal year | |
| Earth's gravity | Earth's radius | |
| 9.806 65 m/s2 | 6 375 km | |

Robert Hooke had published his concept of gravitational forces in 1674, stating that all celestial bodies have an attraction or gravitating power towards their own centers, and also attract all the other celestial bodies that are within the sphere of their activity. He further stated that gravitational attraction increases by how much nearer the body wrought upon is to its own center.[15] In correspondence with Isaac Newton from 1679 and 1680, Hooke conjectured that gravitational forces might decrease according to the double of the distance between the two bodies.[16] Hooke urged Newton, who was a pioneer in the development of calculus, to work through the mathematical details of Keplerian orbits to determine if Hooke's hypothesis was correct. Newton's own investigations verified that Hooke was correct, but due to personal differences between the two men, Newton chose not to reveal this to Hooke. Isaac Newton kept quiet about his discoveries until 1684, at which time he told a friend, Edmond Halley, that he had solved the problem of gravitational orbits, but had misplaced the solution in his office.[17] After being encouraged by Halley, Newton decided to develop his ideas about gravity and publish all of his findings. In November 1684, Isaac Newton sent a document to Edmund Halley, now lost but presumed to have been titled De motu corporum in gyrum (Latin for "On the motion of bodies in an orbit").[18] Halley presented Newton's findings to the Royal Society of London, with a promise that a fuller presentation would follow. Newton later recorded his ideas in a three-book set, entitled Philosophiæ Naturalis Principia Mathematica (English: Mathematical Principles of Natural Philosophy). The first was received by the Royal Society on 28 April 1685–86; the second on 2 March 1686–87; and the third on 6 April 1686–87. The Royal Society published Newton's entire collection at their own expense in May 1686–87.[19]: 31
Isaac Newton had bridged the gap between Kepler's gravitational mass and Galileo's gravitational acceleration, resulting in the discovery of the following relationship which governed both of these:
where g is the apparent acceleration of a body as it passes through a region of space where gravitational fields exist, μ is the gravitational mass (standard gravitational parameter) of the body causing gravitational fields, and R is the radial coordinate (the distance between the centers of the two bodies).
By finding the exact relationship between a body's gravitational mass and its gravitational field, Newton provided a second method for measuring gravitational mass. The mass of the Earth can be determined using Kepler's method (from the orbit of Earth's Moon), or it can be determined by measuring the gravitational acceleration on the Earth's surface, and multiplying that by the square of the Earth's radius. The mass of the Earth is approximately three-millionths of the mass of the Sun. To date, no other accurate method for measuring gravitational mass has been discovered.[20]
Newton's cannonball
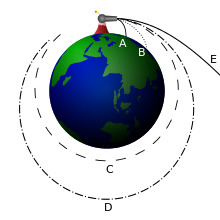
Newton's cannonball was a thought experiment used to bridge the gap between Galileo's gravitational acceleration and Kepler's elliptical orbits. It appeared in Newton's 1728 book A Treatise of the System of the World. According to Galileo's concept of gravitation, a dropped stone falls with constant acceleration down towards the Earth. However, Newton explains that when a stone is thrown horizontally (meaning sideways or perpendicular to Earth's gravity) it follows a curved path. "For a stone projected is by the pressure of its own weight forced out of the rectilinear path, which by the projection alone it should have pursued, and made to describe a curve line in the air; and through that crooked way is at last brought down to the ground. And the greater the velocity is with which it is projected, the farther it goes before it falls to the Earth."[19]: 513 Newton further reasons that if an object were "projected in an horizontal direction from the top of a high mountain" with sufficient velocity, "it would reach at last quite beyond the circumference of the Earth, and return to the mountain from which it was projected."[21]
Universal gravitational mass
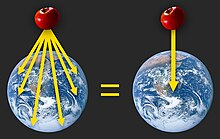
In contrast to earlier theories (e.g. celestial spheres) which stated that the heavens were made of entirely different material, Newton's theory of mass was groundbreaking partly because it introduced universal gravitational mass: every object has gravitational mass, and therefore, every object generates a gravitational field. Newton further assumed that the strength of each object's gravitational field would decrease according to the square of the distance to that object. If a large collection of small objects were formed into a giant spherical body such as the Earth or Sun, Newton calculated the collection would create a gravitational field proportional to the total mass of the body,[19]: 397 and inversely proportional to the square of the distance to the body's center.[19]: 221 [note 7]
For example, according to Newton's theory of universal gravitation, each carob seed produces a gravitational field. Therefore, if one were to gather an immense number of carob seeds and form them into an enormous sphere, then the gravitational field of the sphere would be proportional to the number of carob seeds in the sphere. Hence, it should be theoretically possible to determine the exact number of carob seeds that would be required to produce a gravitational field similar to that of the Earth or Sun. In fact, by unit conversion it is a simple matter of abstraction to realize that any traditional mass unit can theoretically be used to measure gravitational mass.

Measuring gravitational mass in terms of traditional mass units is simple in principle, but extremely difficult in practice. According to Newton's theory, all objects produce gravitational fields and it is theoretically possible to collect an immense number of small objects and form them into an enormous gravitating sphere. However, from a practical standpoint, the gravitational fields of small objects are extremely weak and difficult to measure. Newton's books on universal gravitation were published in the 1680s, but the first successful measurement of the Earth's mass in terms of traditional mass units, the Cavendish experiment, did not occur until 1797, over a hundred years later. Henry Cavendish found that the Earth's density was 5.448 ± 0.033 times that of water. As of 2009, the Earth's mass in kilograms is only known to around five digits of accuracy, whereas its gravitational mass is known to over nine significant figures.[clarification needed]
Given two objects A and B, of masses MA and MB, separated by a displacement RAB, Newton's law of gravitation states that each object exerts a gravitational force on the other, of magnitude
- ,
where G is the universal gravitational constant. The above statement may be reformulated in the following way: if g is the magnitude at a given location in a gravitational field, then the gravitational force on an object with gravitational mass M is
- .
This is the basis by which masses are determined by weighing. In simple spring scales, for example, the force F is proportional to the displacement of the spring beneath the weighing pan, as per Hooke's law, and the scales are calibrated to take g into account, allowing the mass M to be read off. Assuming the gravitational field is equivalent on both sides of the balance, a balance measures relative weight, giving the relative gravitation mass of each object.
Inertial mass
Mass was traditionally believed to be a measure of the quantity of matter in a physical body, equal to the "amount of matter" in an object. For example, Barre´ de Saint-Venant argued in 1851 that every object contains a number of "points" (basically, interchangeable elementary particles), and that mass is proportional to the number of points the object contains.[22] (In practice, this "amount of matter" definition is adequate for most of classical mechanics, and sometimes remains in use in basic education, if the priority is to teach the difference between mass from weight.)[23] This traditional "amount of matter" belief was contradicted by the fact that different atoms (and, later, different elementary particles) can have different masses, and was further contradicted by Einstein's theory of relativity (1905), which showed that the measurable mass of an object increases when energy is added to it (for example, by increasing its temperature or forcing it near an object that electrically repels it.) This motivates a search for a different definition of mass that is more accurate than the traditional definition of "the amount of matter in an object".[24]

Inertial mass is the mass of an object measured by its resistance to acceleration. This definition has been championed by Ernst Mach[25][26] and has since been developed into the notion of operationalism by Percy W. Bridgman.[27][28] The simple classical mechanics definition of mass differs slightly from the definition in the theory of special relativity, but the essential meaning is the same.
In classical mechanics, according to Newton's second law, we say that a body has a mass m if, at any instant of time, it obeys the equation of motion
where F is the resultant force acting on the body and a is the acceleration of the body's centre of mass.[note 8] For the moment, we will put aside the question of what "force acting on the body" actually means.
This equation illustrates how mass relates to the inertia of a body. Consider two objects with different masses. If we apply an identical force to each, the object with a bigger mass will experience a smaller acceleration, and the object with a smaller mass will experience a bigger acceleration. We might say that the larger mass exerts a greater "resistance" to changing its state of motion in response to the force.
However, this notion of applying "identical" forces to different objects brings us back to the fact that we have not really defined what a force is. We can sidestep this difficulty with the help of Newton's third law, which states that if one object exerts a force on a second object, it will experience an equal and opposite force. To be precise, suppose we have two objects of constant inertial masses m1 and m2. We isolate the two objects from all other physical influences, so that the only forces present are the force exerted on m1 by m2, which we denote F12, and the force exerted on m2 by m1, which we denote F21. Newton's second law states that
where a1 and a2 are the accelerations of m1 and m2, respectively. Suppose that these accelerations are non-zero, so that the forces between the two objects are non-zero. This occurs, for example, if the two objects are in the process of colliding with one another. Newton's third law then states that
and thus
If |a1| is non-zero, the fraction is well-defined, which allows us to measure the inertial mass of m1. In this case, m2 is our "reference" object, and we can define its mass m as (say) 1 kilogram. Then we can measure the mass of any other object in the universe by colliding it with the reference object and measuring the accelerations.
Additionally, mass relates a body's momentum p to its linear velocity v:
and the body's kinetic energy K to its velocity:
The primary difficulty with Mach's definition of mass is that it fails to take into account the potential energy (or binding energy) needed to bring two masses sufficiently close to one another to perform the measurement of mass.[26] This is most vividly demonstrated by comparing the mass of the proton in the nucleus of deuterium, to the mass of the proton in free space (which is greater by about 0.239%—this is due to the binding energy of deuterium). Thus, for example, if the reference weight m2 is taken to be the mass of the neutron in free space, and the relative accelerations for the proton and neutron in deuterium are computed, then the above formula over-estimates the mass m1 (by 0.239%) for the proton in deuterium. At best, Mach's formula can only be used to obtain ratios of masses, that is, as m1 / m2 = |a2| / |a1|. An additional difficulty was pointed out by Henri Poincaré, which is that the measurement of instantaneous acceleration is impossible: unlike the measurement of time or distance, there is no way to measure acceleration with a single measurement; one must make multiple measurements (of position, time, etc.) and perform a computation to obtain the acceleration. Poincaré termed this to be an "insurmountable flaw" in the Mach definition of mass.[29]
Atomic masses
Typically, the mass of objects is measured in terms of the kilogram, which since 2019 is defined in terms of fundamental constants of nature. The mass of an atom or other particle can be compared more precisely and more conveniently to that of another atom, and thus scientists developed the dalton (also known as the unified atomic mass unit). By definition, 1 Da (one dalton) is exactly one-twelfth of the mass of a carbon-12 atom, and thus, a carbon-12 atom has a mass of exactly 12 Da.
In relativity
Special relativity
In some frameworks of special relativity, physicists have used different definitions of the term. In these frameworks, two kinds of mass are defined: rest mass (invariant mass),[note 9] and relativistic mass (which increases with velocity). Rest mass is the Newtonian mass as measured by an observer moving along with the object. Relativistic mass is the total quantity of energy in a body or system divided by c2. The two are related by the following equation:
where is the Lorentz factor:
The invariant mass of systems is the same for observers in all inertial frames, while the relativistic mass depends on the observer's frame of reference. In order to formulate the equations of physics such that mass values do not change between observers, it is convenient to use rest mass. The rest mass of a body is also related to its energy E and the magnitude of its momentum p by the relativistic energy-momentum equation:
So long as the system is closed with respect to mass and energy, both kinds of mass are conserved in any given frame of reference. The conservation of mass holds even as some types of particles are converted to others. Matter particles (such as atoms) may be converted to non-matter particles (such as photons of light), but this does not affect the total amount of mass or energy. Although things like heat may not be matter, all types of energy still continue to exhibit mass.[note 10][30] Thus, mass and energy do not change into one another in relativity; rather, both are names for the same thing, and neither mass nor energy appear without the other.
Both rest and relativistic mass can be expressed as an energy by applying the well-known relationship E = mc2, yielding rest energy and "relativistic energy" (total system energy) respectively:
The "relativistic" mass and energy concepts are related to their "rest" counterparts, but they do not have the same value as their rest counterparts in systems where there is a net momentum. Because the relativistic mass is proportional to the energy, it has gradually fallen into disuse among physicists.[31] There is disagreement over whether the concept remains useful pedagogically.[32][33][34]
In bound systems, the binding energy must often be subtracted from the mass of the unbound system, because binding energy commonly leaves the system at the time it is bound. The mass of the system changes in this process merely because the system was not closed during the binding process, so the energy escaped. For example, the binding energy of atomic nuclei is often lost in the form of gamma rays when the nuclei are formed, leaving nuclides which have less mass than the free particles (nucleons) of which they are composed.
Mass–energy equivalence also holds in macroscopic systems.[35] For example, if one takes exactly one kilogram of ice, and applies heat, the mass of the resulting melt-water will be more than a kilogram: it will include the mass from the thermal energy (latent heat) used to melt the ice; this follows from the conservation of energy.[36] This number is small but not negligible: about 3.7 nanograms. It is given by the latent heat of melting ice (334 kJ/kg) divided by the speed of light squared (c2 ≈ 9×1016 m2/s2).
General relativity
In general relativity, the equivalence principle is the equivalence of gravitational and inertial mass. At the core of this assertion is Albert Einstein's idea that the gravitational force as experienced locally while standing on a massive body (such as the Earth) is the same as the pseudo-force experienced by an observer in a non-inertial (i.e. accelerated) frame of reference.
However, it turns out that it is impossible to find an objective general definition for the concept of invariant mass in general relativity. At the core of the problem is the non-linearity of the Einstein field equations, making it impossible to write the gravitational field energy as part of the stress–energy tensor in a way that is invariant for all observers. For a given observer, this can be achieved by the stress–energy–momentum pseudotensor.[37]
In quantum physics
In classical mechanics, the inert mass of a particle appears in the Euler–Lagrange equation as a parameter m:
After quantization, replacing the position vector x with a wave function, the parameter m appears in the kinetic energy operator:
In the ostensibly covariant (relativistically invariant) Dirac equation, and in natural units, this becomes:
where the "mass" parameter m is now simply a constant associated with the quantum described by the wave function ψ.
In the Standard Model of particle physics as developed in the 1960s, this term arises from the coupling of the field ψ to an additional field Φ, the Higgs field. In the case of fermions, the Higgs mechanism results in the replacement of the term mψ in the Lagrangian with . This shifts the explanandum of the value for the mass of each elementary particle to the value of the unknown coupling constant Gψ.
Tachyonic particles and imaginary (complex) mass
A tachyonic field, or simply tachyon, is a quantum field with an imaginary mass.[38] Although tachyons (particles that move faster than light) are a purely hypothetical concept not generally believed to exist,[38][39] fields with imaginary mass have come to play an important role in modern physics[40][41][42] and are discussed in popular books on physics.[38][43] Under no circumstances do any excitations ever propagate faster than light in such theories—the presence or absence of a tachyonic mass has no effect whatsoever on the maximum velocity of signals (there is no violation of causality).[44] While the field may have imaginary mass, any physical particles do not; the "imaginary mass" shows that the system becomes unstable, and sheds the instability by undergoing a type of phase transition called tachyon condensation (closely related to second order phase transitions) that results in symmetry breaking in current models of particle physics.
The term "tachyon" was coined by Gerald Feinberg in a 1967 paper,[45] but it was soon realized that Feinberg's model in fact did not allow for superluminal speeds.[44] Instead, the imaginary mass creates an instability in the configuration:- any configuration in which one or more field excitations are tachyonic will spontaneously decay, and the resulting configuration contains no physical tachyons. This process is known as tachyon condensation. Well known examples include the condensation of the Higgs boson in particle physics, and ferromagnetism in condensed matter physics.
Although the notion of a tachyonic imaginary mass might seem troubling because there is no classical interpretation of an imaginary mass, the mass is not quantized. Rather, the scalar field is; even for tachyonic quantum fields, the field operators at spacelike separated points still commute (or anticommute), thus preserving causality. Therefore, information still does not propagate faster than light,[45] and solutions grow exponentially, but not superluminally (there is no violation of causality). Tachyon condensation drives a physical system that has reached a local limit and might naively be expected to produce physical tachyons, to an alternate stable state where no physical tachyons exist. Once the tachyonic field reaches the minimum of the potential, its quanta are not tachyons any more but rather are ordinary particles with a positive mass-squared.[46]
This is a special case of the general rule, where unstable massive particles are formally described as having a complex mass, with the real part being their mass in the usual sense, and the imaginary part being the decay rate in natural units.[46] However, in quantum field theory, a particle (a "one-particle state") is roughly defined as a state which is constant over time; i.e., an eigenvalue of the Hamiltonian. An unstable particle is a state which is only approximately constant over time; If it exists long enough to be measured, it can be formally described as having a complex mass, with the real part of the mass greater than its imaginary part. If both parts are of the same magnitude, this is interpreted as a resonance appearing in a scattering process rather than a particle, as it is considered not to exist long enough to be measured independently of the scattering process. In the case of a tachyon, the real part of the mass is zero, and hence no concept of a particle can be attributed to it.
In a Lorentz invariant theory, the same formulas that apply to ordinary slower-than-light particles (sometimes called "bradyons" in discussions of tachyons) must also apply to tachyons. In particular the energy–momentum relation:
(where p is the relativistic momentum of the bradyon and m is its rest mass) should still apply, along with the formula for the total energy of a particle:
This equation shows that the total energy of a particle (bradyon or tachyon) contains a contribution from its rest mass (the "rest mass–energy") and a contribution from its motion, the kinetic energy. When v is larger than c, the denominator in the equation for the energy is "imaginary", as the value under the radical is negative. Because the total energy must be real, the numerator must also be imaginary: i.e. the rest mass m must be imaginary, as a pure imaginary number divided by another pure imaginary number is a real number.
See also
Notes
- ^ When a distinction is necessary, the active and passive gravitational masses may be distinguished.
- ^ The dalton is convenient for expressing the masses of atoms and molecules.
- ^ These are used mainly in the United States except in scientific contexts where SI units are usually used instead.
- ^ The distinction between "active" and "passive" gravitational mass does not exist in the Newtonian view of gravity as found in classical mechanics, and can safely be ignored for many purposes. In most practical applications, Newtonian gravity is assumed because it is usually sufficiently accurate, and is simpler than General Relativity; for example, NASA uses primarily Newtonian gravity to design space missions, although "accuracies are routinely enhanced by accounting for tiny relativistic effects".www2
.jpl .nasa .gov /basics /bsf3-2 .php The distinction between "active" and "passive" is very abstract, and applies to post-graduate level applications of General Relativity to certain problems in cosmology, and is otherwise not used. There is, nevertheless, an important conceptual distinction in Newtonian physics between "inertial mass" and "gravitational mass", although these quantities are identical; the conceptual distinction between these two fundamental definitions of mass is maintained for teaching purposes because they involve two distinct methods of measurement. It was long considered anomalous that the two distinct measurements of mass (inertial and gravitational) gave an identical result. The property, observed by Galileo, that objects of different mass fall with the same rate of acceleration (ignoring air resistance), shows that inertial and gravitational mass are the same. - ^ This constant ratio was later shown to be a direct measure of the Sun's active gravitational mass; it has units of distance cubed per time squared, and is known as the standard gravitational parameter:
- ^ At the time when Viviani asserts that the experiment took place, Galileo had not yet formulated the final version of his law of free fall. He had, however, formulated an earlier version that predicted that bodies of the same material falling through the same medium would fall at the same speed. See Drake, S. (1978). Galileo at Work. University of Chicago Press. pp. 19–20. ISBN 978-0-226-16226-3.
- ^ These two properties are very useful, as they allow spherical collections of objects to be treated exactly like large individual objects.
- ^ In its original form, Newton's second law is valid only for bodies of constant mass.
- ^ It is possible to make a slight distinction between "rest mass" and "invariant mass". For a system of two or more particles, none of the particles are required be at rest with respect to the observer for the system as a whole to be at rest with respect to the observer. To avoid this confusion, some sources will use "rest mass" only for individual particles, and "invariant mass" for systems.
- ^ For example, a nuclear bomb in an idealized super-strong box, sitting on a scale, would in theory show no change in mass when detonated (although the inside of the box would become much hotter). In such a system, the mass of the box would change only if energy were allowed to escape from the box as light or heat. However, in that case, the removed energy would take its associated mass with it. Letting heat or radiation out of such a system is simply a way to remove mass. Thus, mass, like energy, cannot be destroyed, but only moved from one place to another.
References
- ^ Bray, Nancy (28 April 2015). "Science". NASA. Archived from the original on 30 May 2023. Retrieved 20 March 2023.
Mass can be understood as a measurement of inertia, the resistance of an object to be set in motion or stopped from motion.
- ^ "The Higgs boson". CERN. 3 April 2024. Retrieved 9 April 2024.
- ^ "New Quantum Theory Separates Gravitational and Inertial Mass". MIT Technology Review. 14 June 2010. Retrieved 25 September 2020.
- ^ von Klitzing, Klaus (February 2017). "Metrology in 2019" (PDF). Nature Physics. 13 (2): 198. arXiv:1707.06785. Bibcode:2017SSPMA..47l9503L. doi:10.1360/SSPMA2017-00044. S2CID 133817316.
- ^ "Draft of the ninth SI Brochure" (PDF). BIPM. 10 November 2016. pp. 2–9. Retrieved 10 September 2017.
- ^ W. Rindler (2006). Relativity: Special, General, And Cosmological. Oxford University Press. pp. 16–18. ISBN 978-0-19-856731-8.
- ^ Kane, Gordon (4 September 2008). "The Mysteries of Mass". Scientific American. Nature America, Inc. pp. 32–39. Retrieved 5 July 2013.
- ^ Eötvös, R.V.; Pekár, D.; Fekete, E. (1922). "Beiträge zum Gesetz der Proportionalität von Trägheit und Gravität" (PDF). Annalen der Physik. 68 (9): 11–66. Bibcode:1922AnP...373...11E. doi:10.1002/andp.19223730903.
- ^ Voisin, G.; Cognard, I.; Freire, P. C. C.; Wex, N.; Guillemot, L.; Desvignes, G.; Kramer, M.; Theureau, G. (June 2020). "An improved test of the strong equivalence principle with the pulsar in a triple star system". Astronomy & Astrophysics. 638: A24. arXiv:2005.01388. Bibcode:2020A&A...638A..24V. doi:10.1051/0004-6361/202038104. S2CID 218486794. Retrieved 4 May 2022.
- ^ a b Browne, K. M. (2018). "The pre-Newtonian meaning of the word "weight"; a comment on "Kepler and the origins of pre-Newtonian mass" [Am. J. Phys. 85, 115–123 (2017)]". American Journal of Physics. 86 (6): 471–74. Bibcode:2018AmJPh..86..471B. doi:10.1119/1.5027490. S2CID 125953814.
- ^ Drake, S. (1979). "Galileo's Discovery of the Law of Free Fall". Scientific American. 228 (5): 84–92. Bibcode:1973SciAm.228e..84D. doi:10.1038/scientificamerican0573-84.
- ^ Galileo, G. (1632). Dialogue Concerning the Two Chief World Systems.
- ^ Galileo, G. (1638). Discorsi e Dimostrazioni Matematiche, Intorno à Due Nuove Scienze. Vol. 213. Louis Elsevier., translated in Crew, H.; de Salvio, A., eds. (1954). Mathematical Discourses and Demonstrations, Relating to Two New Sciences. Dover Publications. ISBN 978-1-275-10057-2. Archived from the original on 1 October 2013. Retrieved 11 April 2012. and also available in Hawking, S., ed. (2002). On the Shoulders of Giants. Running Press. pp. 534–535. ISBN 978-0-7624-1348-5.
- ^ Newton, I. (1729) [1686]. The mathematical principles of natural philosophy. Translated by Motte, A. Printed for Benjamin Motte. pp. 1–2.
- ^ Hooke, R. (1674). An attempt to prove the motion of the earth from observations. Royal Society.
- ^ Turnbull, H.W., ed. (1960). Correspondence of Isaac Newton, Volume 2 (1676–1687). Cambridge University Press. p. 297.
- ^ Principia (PDF). p. 16.
- ^ Whiteside, D.T., ed. (2008). The Mathematical Papers of Isaac Newton, Volume VI (1684–1691). Cambridge University Press. ISBN 978-0-521-04585-8.
- ^ a b c d Sir Isaac Newton; N.W. Chittenden (1848). Newton's Principia: The mathematical principles of natural philosophy. D. Adee. p. 31. ISBN 9780520009295.
- ^ Cuk, M. (January 2003). "Curious About Astronomy: How do you measure a planet's mass?". Ask an Astronomer. Archived from the original on 20 March 2003. Retrieved 12 March 2011.
- ^ Newton, Isaac (1728). A Treatise of the System of the World. London: F. Fayram. p. 6. Retrieved 4 May 2022.
- ^ Coelho, Ricardo Lopes (January 2010). "On the Concept of Force: How Understanding its History can Improve Physics Teaching". Science & Education. 19 (1): 91–113. Bibcode:2010Sc&Ed..19...91C. doi:10.1007/s11191-008-9183-1. S2CID 195229870.
- ^ Gibbs, Yvonne (31 March 2017). "Teachers Learn the Difference Between Mass and Weight Even in Space". NASA. Archived from the original on 20 March 2023. Retrieved 20 March 2023.
- ^ Hecht, Eugene (January 2006). "There Is No Really Good Definition of Mass". The Physics Teacher. 44 (1): 40–45. Bibcode:2006PhTea..44...40H. doi:10.1119/1.2150758.
- ^ Ernst Mach, "Science of Mechanics" (1919)
- ^ a b Ori Belkind, "Physical Systems: Conceptual Pathways between Flat Space-time and Matter" (2012) Springer (Chapter 5.3)
- ^ P.W. Bridgman, Einstein's Theories and the Operational Point of View, in: P.A. Schilpp, ed., Albert Einstein: Philosopher-Scientist, Open Court, La Salle, Ill., Cambridge University Press, 1982, Vol. 2, pp. 335–354.
- ^ Gillies, D.A. (1972). "PDF" (PDF). Synthese. 25: 1–24. doi:10.1007/BF00484997. S2CID 239369276. Archived from the original (PDF) on 26 April 2016. Retrieved 10 April 2016.
- ^ Henri Poincaré. "Classical Mechanics". Chapter 6 in Science and Hypothesis. London: Walter Scott Publishing (1905): 89-110.
- ^ Taylor, E.F.; Wheeler, J.A. (1992). Spacetime Physics. W.H. Freeman. pp. 248–149. ISBN 978-0-7167-2327-1.
- ^ G. Oas (2005). "On the Abuse and Use of Relativistic Mass". arXiv:physics/0504110.
- ^ Okun, L.B. (1989). "The Concept of Mass" (PDF). Physics Today. 42 (6): 31–36. Bibcode:1989PhT....42f..31O. doi:10.1063/1.881171. Archived from the original (PDF) on 22 July 2011.
- ^ Rindler, W.; Vandyck, M.A.; Murugesan, P.; Ruschin, S.; Sauter, C.; Okun, L.B. (1990). "Putting to Rest Mass Misconceptions" (PDF). Physics Today. 43 (5): 13–14, 115, 117. Bibcode:1990PhT....43e..13R. doi:10.1063/1.2810555. Archived from the original (PDF) on 22 July 2011.
- ^ Sandin, T.R. (1991). "In Defense of Relativistic Mass". American Journal of Physics. 59 (11): 1032. Bibcode:1991AmJPh..59.1032S. doi:10.1119/1.16642.
- ^ Planck, Max (1907), "Zur Dynamik bewegter Systeme", Sitzungsberichte der Königlich-Preussischen Akademie der Wissenschaften, Berlin, Erster Halbband (29): 542–570, Bibcode:1908AnP...331....1P, doi:10.1002/andp.19083310602
- English Wikisource translation: On the Dynamics of Moving Systems (See paragraph 16.)
- ^ Hecht, Eugene (2006). "There Is No Really Good Definition of Mass" (PDF). The Physics Teacher. 44 (1): 40–45. Bibcode:2006PhTea..44...40H. doi:10.1119/1.2150758.
- ^ Misner, C.W.; Thorne, K.S.; Wheeler, J.A. (1973). Gravitation. W.H. Freeman. p. 466. ISBN 978-0-7167-0344-0.
- ^ a b c Lisa Randall, Warped Passages: Unraveling the Mysteries of the Universe's Hidden Dimensions, p.286: "People initially thought of tachyons as particles travelling faster than the speed of light...But we now know that a tachyon indicates an instability in a theory that contains it. Regrettably for science fiction fans, tachyons are not real physical particles that appear in nature."
- ^ Tipler, Paul A.; Llewellyn, Ralph A. (2008). Modern Physics (5th ed.). New York: W.H. Freeman & Co. p. 54. ISBN 978-0-7167-7550-8.
... so existence of particles v > c ... Called tachyons ... would present relativity with serious ... problems of infinite creation energies and causality paradoxes.
- ^ Kutasov, David; Marino, Marcos & Moore, Gregory W. (2000). "Some exact results on tachyon condensation in string field theory". Journal of High Energy Physics. 2000 (10): 045. arXiv:hep-th/0009148. Bibcode:2000JHEP...10..045K. doi:10.1088/1126-6708/2000/10/045. S2CID 15664546.
- ^ Sen, Ashoke (2002). "Rolling Tachyon". Journal of High Energy Physics. 2002 (4): 048. arXiv:hep-th/0203211. Bibcode:2002JHEP...04..048S. doi:10.1088/1126-6708/2002/04/048. S2CID 12023565.
- ^ Gibbons, G.W. (2002). "Cosmological evolution of the rolling tachyon". Phys. Lett. B. 537 (1–2): 1–4. arXiv:hep-th/0204008. Bibcode:2002PhLB..537....1G. doi:10.1016/s0370-2693(02)01881-6. S2CID 119487619.
- ^ Greene, Brian (2000). The Elegant Universe. Vintage Books.
- ^ a b Aharonov, Y.; Komar, A.; Susskind, L. (1969). "Superluminal Behavior, Causality, and Instability". Phys. Rev. 182 (5): 1400–1403. Bibcode:1969PhRv..182.1400A. doi:10.1103/PhysRev.182.1400.
- ^ a b Feinberg, Gerald (1967). "Possibility of Faster-Than-Light Particles". Physical Review. 159 (5): 1089–1105. Bibcode:1967PhRv..159.1089F. doi:10.1103/PhysRev.159.1089.
- ^ a b Peskin, M.E.; Schroeder, D.V. (1995). An Introduction to Quantum Field Theory. Perseus Books.
External links
- Francisco Flores (6 February 2012). "The Equivalence of Mass and Energy". Stanford Encyclopedia of Philosophy.
- Gordon Kane (27 June 2005). "The Mysteries of Mass". Scientific American. Archived from the original on 10 October 2007.
- L.B. Okun (2002). "Photons, Clocks, Gravity and the Concept of Mass". Nuclear Physics B: Proceedings Supplements. 110: 151–155. arXiv:physics/0111134. Bibcode:2002NuPhS.110..151O. doi:10.1016/S0920-5632(02)01472-X. S2CID 16733517.
- Frank Wilczek (13 May 2001). "The Origin of Mass and the Feebleness of Gravity" (video). MIT Video.
- John Baez; et al. (2012). "Does mass change with velocity?".
- John Baez; et al. (2008). "What is the mass of a photon?".
- Jim Baggott (27 September 2017). The Concept of Mass (video) published by the Royal Institution on YouTube.


































