Talk:Dymaxion map

Untitled

See meta:Spacetime DTD and meta:Ecoregion DTD

Peters Projection

Is Dymaxion Map the same as the Peters Projection map of the world? quercus robur

no, it is not at all the same from what I just saw (http://www.petersmap.com/page2.html, mercator on the right, Peters on the left). I left an example of the dymaxion map on the article page (see animation - ain't that pretty ?). If I understood well, one of the ideas is that no continent should be cut by the projection, that all terrestrial masses appear in one mass (?), and a better accuracy (less deformed than mercantur map in particular). User:anthere

List of links

http://worldgame.org/

saving links needed to work on this map

animation (free)

http://www.westnet.com/~crywalt/unfold.html

http://www.nous.org.uk/BFMAP.html

The first item is a piece of text (not a link), the second is in the article, and third is a general article on Fuller, not on his map. -º¡º

move your eyes at the top of this page. This article is part of a wikiproject. As such, a little bit more information is required.

And? Nothing was deleted from the talk, I was just commenting. -º¡º

Neutrality

Neutrality here? How about some negatives, like the fact that it confuses navigation (North is in the center, rather than at an extreme).

Yeah, agree. Why no negative points. Like "difficult to compare % of land and sea", "unability to quickly see tropical belt" etc. ? Peter S. 02:33, 10 October 2005 (UTC)

The fact that it's encumbered with copyrights and is not supposed to show nations as colored regions is a key disadvantage from the point of view of those wishing to publish political maps. Fortunately, many other mapping frameworks are available for this purpose.

Also, talking of seafaring nations - try to show on this map how Columbus found his way to America... — Preceding unsigned comment added by 119.98.18.179 (talk) 04:46, 24 November 2011 (UTC)

Alternative layouts

This icosahedral net shows connected oceans surrounding Antarctica

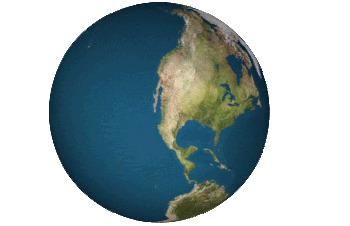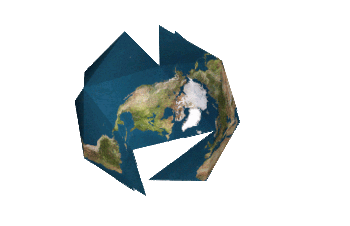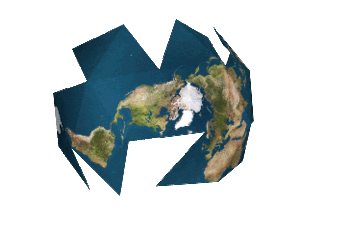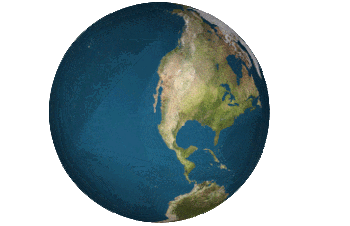
"There is no one 'correct' view of the Dymaxion map. Peeling the triangular faces of the icosahedron apart in one way results in an icosahedral net that shows an almost contiguous land mass comprising all of earth's continents - not groups of continents divided by oceans. Peeling the solid apart in a different way presents a view of the world dominated by connected oceans surrounded by land."

Would it be possible for someone to make an example of the second view,where oceans dominate?

 Done.

So... how does the math work?

So... if I have the some coordinates of a point on a surface, how would I transform those points to find the coordinates of the corresponding position on a dymaxion map? (Pick one, though I am specifically interested in polyhedral dymaxion maps – let's say a dymaxion map based on a regular octohedron.) —Preceding unsigned comment added by 71.126.169.10 (talk) 22:52, 6 August 2008 (UTC)

I know this was 10 years ago, but if anyone is curious, the only mention of the exact equations I could find was Robert Gray. According to him, it comes down to conserving distances along the icosohedron edges and then interpolating using a three-way geodesic grid. The math gets pretty complicated. Justin Kunimune (talk) 03:05, 21 January 2018 (UTC)

Conformal?

An icosohedron has 20 faces. 20 separate stereographic projections—one for each of the 20 faces—would seem to be what's going on. That would make it conformal except at the 12 vertices. Can someone with experience with these maps comment on this? Michael Hardy (talk) 22:38, 17 October 2009 (UTC)

...Wait!... maybe it would be conformal except on the edges.

If so, that raises the question of whether there is some other way to do it that would make it conformal except at the vertices. Michael Hardy (talk) 22:56, 17 October 2009 (UTC)

....on the other hand one could project from the center of the sphere, rather from the point antipodal to the point of tangency, and that seems quite natural. But I don't know if it's conformal.... Michael Hardy (talk) 18:17, 18 October 2009 (UTC)

The radial projection (from the south hemisphere S₊ to C, seen as the tangent plane at the south pole) is not conformal. Reason : if it were conformal, we could compose the inverse of the radial projection, C → S₊, with the standard stereographic projection S → C; the result would be a radial holomorphic map C →C, that is, of the form f(re^it)=φ(r)e^it, which can be holomorphic only if f(z)=az, which is not the case here. Alternatively, it would be a bounded holomorphic map on C, hence constant by Liouville theorem, again not the case here. (moved from RD/M) --pma (talk) 08:04, 23 October 2009 (UTC)

"that raises the question of whether there is some other way to do it" Yes. Whatever particular projection the standard Dymaxion map uses, we can imagine developing some other map that is almost identical to the Dymaxion map, except it uses some other projection:

• I hear that Laurence P. Lee of New Zealand developed a conformal mapping that can be used to map spherical triangles to plane triangles. So yes, there is a way to make it conformal, except at the vertices. Is there any Wikipedia article that would be appropriate for posting the details of this projection?
• stereographic projection: each facet is conformal. Unfortunately, stereographic projection maps the 3 great circle arcs bounding each spherical triangle to 3 "lines" that gently curve (bulge out), so there's going to be a bit of mangling to make a straight-edged plane triangle; so I guess the edges are not exactly conformal.
• gnomonic projection -- one could project from the center of the sphere. That is used for *most* polygonal maps (but not the Dymaxion map). Alas, it is not conformal, as PMajer pointed out. It does have the great advantage that great circles map to straight lines, so spherical triangles map nicely to straight-edged plane triangles.
• the Chamberlin trimetric projection sounds very similar to the projection described for the Dymaxion map. Is there any significant difference?
• I hear that Irving Fisher developed an equal-area mapping that exactly covers the icosahedron; and John P. Snyder generalized that mapping, now called the Fisher/Snyder equal-area mapping. Alas, all equal-area mappings are not conformal, and vice versa. Is there any Wikipedia article that would be appropriate for posting the details of this projection?

--68.0.124.33 (talk) 23:08, 21 July 2010 (UTC)

This looks like supremely helpful information which ought to be in the article - I've just left a note over at Chamberlin trimetric projection querying whether that's the projection used for the Dymaxion. I think it'd be the most accurate - adjacent vertices would match up - but I'm no cartographer! Any chance of someone with a Big Book of Projections clarifying this in the article? 87.194.176.188 (talk) 17:24, 2 July 2011 (UTC)

Geocart has a conformal version of the dymaxion. Strebe (talk) 17:42, 13 September 2019 (UTC)

File:Dymaxion 2003 animation small1.gif to appear as POTD soon

Hello! This is a note to let the editors of this article know that File:Dymaxion 2003 animation small1.gif will be appearing as picture of the day on June 5, 2011. You can view and edit the POTD blurb at Template:POTD/2011-06-05. If this article needs any attention or maintenance, it would be preferable if that could be done before its appearance on the Main Page so Wikipedia doesn't look bad. :) Thanks! howcheng {chat} 17:53, 2 June 2011 (UTC)

Picture of the day

An animation showing the unfolding of a Dymaxion map, a projection of a world map onto the surface of a polyhedron (in this case, an icosahedron) and then flattened to form a two-dimensional map which retains most of the relative proportional integrity of the globe map. This type of map was invented by Buckminster Fuller and is one of several of his inventions to use the name Dymaxion.Image: Chris Rywalt

Keyes promoting his stuff

Esperanto41 is attempting to inject his opinion piece as an external link. His rationale for reverting my deletion was, “Restored link to Web's most extensively detailed history, analysis, and critique of Fuller's map.” The article he links is just a personal opinion piece, violating WP:RELY and WP:USERG. It’s his own work, violating WP:COI and WP:SELFPUBLISH. It is a mass of rhetoric, devoid of science, data, reliable external references to it, and meanwhile having the tendentious purpose of disparaging the Fuller projection and directing the reader’s attention to the Cahill projection, which he has a vested interest in.

Gene, if you revert this again, I will revert your reversion and request a page lock. There is no question about these policies you are violating.Strebe (talk)

Strebe's conflict of interest

Daan Strebe is a commercial cartography software producer, who feels he can become Wikipedia's self-appointed dictator of approved projections, and disparage or delete those which are not included in his mindset or his proprietary program. Talk about conflict of interest! He waged a vendetta to delete and suppress the octahedral Waterman projection page in Wikipedia. Strebe's commercial program does not include Cahill or Fuller or Waterman, but it does include Strebe's own projections. Again, COI.

Unlike Strebe, I am not a vendor. I do not have a so-called "vested interest" in B.J.S. Cahill, nor in my own revisions to Cahill. My map designs and programs are freely downloadable on the Web, open source and in Creative Commons. I do not object to Strebe's cartographic expertise, and projections, and private enterprise, but I do object to him bringing his prejudices and conflict of interest into a public venue such as Wikipedia, while presuming that he can delete alternative projections on his say-so, then lock out anyone else.

As for my critique of the Fuller map, I cannot believe that daan has done more than glance at it, and then hurl unsubstantiated invective. (Let him address some of its analyses, such as how one should scale a Dymaxion map.) My piece details the history and evolution and shortcomings of Bucky's map, which of course I would not post as a WP article. But as an external link, it belongs in a WP article on the Dymaxion. Readers are entitled to judge for themselves if the article is germane and worthwhile, and not be subject to Strebe's censorship, and lockout threat. — Preceding unsigned comment added by Esperanto41 (talk • contribs) 23:39, 17 July 2013 (UTC)

I am indebted to you for the first mention of my projections and software anywhere on Wikipedia. Thank you. For some reason doing that myself never occurred to me. I’ve simply been too busy engaged in conflicts of interest, such as keeping unencyclopædic material off of Wikipedia, curating a hundred-and-something articles (dozens unrelated to map projections), adding information from credible sources, add citations and footnotes (including the only citation for the Waterman map, which of course you either did not notice or else do not want this audience to know), correcting grammar and syntax, and creating high quality illustrations free for public use—and zounds, now that you mentioned it, none of them are any of my own projections! How could I be so remiss?

What the images are, are illustrations for articles on projections that have notability as defined by Wikipedia. That’s what my edits are about, but I don’t expect you to understand that in a world where you imagine we’re competitors. We’re not. Fighting over map projections is facile. Nobody’s projection is any good in any general sense, including mine, and nobody’s ever will be. That’s the cold, hard mathematics. The very idea that any world projection is “best” is simply medieval.

Your essay is a vanity work. Of course I read it. It’s a collection of cherry-picked arguments that, even with cherry-picking, don’t add up to what you imagine they do. Wikipedia doesn’t link to vanity works. Any goober can write an opinion piece. You have your forum on the Internet. I have mine. Both of those are distinct from Wikipedia, where linking to vanity pieces is not permitted. If you want a critique of your essay, feel free to contact me directly; this is not the place for that. In any case, my own opinion of it is irrelevant here. What’s relevant is that your link violates WP:COI, WP:SELFPUBLISH, WP:RELY, and WP:USERG. Wikipedia editors don’t decide whether something is “germane” or “worthwhile”. They let experts do that and then cite the experts. Strebe (talk) 03:39, 18 July 2013 (UTC)

File:Dymaxion 2003 animation small1.gif is broken

This file doesn't load at all, there's just the broken image icon 151.227.93.223 (talk) 15:10, 20 September 2015 (UTC)

Works fine on Mac OS X browsers and Safari on iOS 9, for example. Strebe (talk) 17:52, 20 September 2015 (UTC)

Yeah, works fine in Opera, Chrome, and IE 10 on Windows 8.1 too. RossPatterson (talk) 00:33, 21 September 2015 (UTC)

BFI owns the "rights" to the projection?

Supposedly the Buckminster Fuller Institute has said: "Thank you for your interest in the Fuller Projection Map™. BFI owns the rights to the projection, and yes, it requires a licensing agreement for use." (bold mine)

Does anyone know what the heck they are talking about? AFAIK their patent ran out a while ago. They have trademarks for the words "Fuller Projection Map" but nothing more. Is this correct? Maybe they are trying to say the entire projection is a trademark? --147.147.121.40 (talk) 06:29, 4 September 2017 (UTC)

In addition I found a note on patent WO 1993003469 A1 which says: "The Dymaxion Map, copyrighted in 1982 by Buckminister Fuller Institute, projects the Earth globe onto 20 identical equilateral triangular segments [...]".

I did not think you could copyright a map projection? --147.147.121.40 (talk) 06:47, 4 September 2017 (UTC)

They can hold copyright on one or a few particular visual maps, but the patent on the technique for deriving that general type of map would have expired long ago, so I really don't see how they can prevent others from making their own maps with using that projection... AnonMoos (talk) 16:56, 6 September 2017 (UTC)

Real-world application

It's probably worth mentioning that this map projection does see some use in the sciences, whenever the continents and their connections (including across Bering Strait) need to be shown and the oceans are not relevant; apart from the genetics map in the article, compare the map in the infobox of Woolly mammoth. --Florian Blaschke (talk) 21:14, 3 February 2021 (UTC)