Talk:AC power

Real, reactive and apparent power

In the UK, the standard term, defined in British Standards, is "Active Power" rather than "Real Power". Most electrical engineering textbooks that I have used use this same term. Hence, I have edited this article to use "Active Power" as the preferred term, while retaining a mention of "Real Power". I hope this does not conflict with usage in other English-speaking countries. 86.142.3.205 (talk) 16:39, 27 June 2010 (UTC)

Real power, reactive power and apparent power should be combined into one article. This is a mess - repetitive and I'm not sure the three articles are even consistent with each other. --Wtshymanski 04:30, 3 Apr 2005 (UTC)

agreed, assuming appropriate redirects. fyi, you seem to imply that the apparent power is the product of the Vrms and Irms only for a sine wave. This is not true. The rms calculation is not waveform dependent, although the phase separation calculation is based on a sine wave. I also find your use of the term "linear" in this context to be somewhat quirky. Specifically, the juxtaposition with containing only... as you might recall, resistance, capacitance, and inductance is a basis set for a waveguide or conductor with linear response. Moreover, it is the equivalent transfer function that is linear, not the network itself. I admit this is a slight nitpicking of usage but linear is a dangerously overloaded term. (unsigned comment by Pearlg)

we probablly wan't to bring in complex power as well especially since apparent power is just the magnitude of complex power. Plugwash 00:39, 22 Apr 2005 (UTC)

ok well i've done it what do you think of the result?

I am very happy with all you've done with this article so far. I have one objection to "Apparent power is handy for rough sizing of generators or wiring, especially when the power factor is close to 1." As it happens apparent power is very important when the power factor is far from 1. Indeed, when the power factor is close to 1, an engineer need only consider the real power for sizing, but as the power factor declines, these calculations must be made on the basis of the apparent power. The turbines suppling energy to a generator operating at 100% efficiency MUST be conveying energy at a power equal to the real power + losses due to the reactive power. From the stand-point of a person or turbine turning the generator the apparent power affects how much power must be generated to deliver the real power. --Pearlg 03:10, 24 Jun 2005 (UTC), --Pearlg 23:07, 24 Jun 2005 (UTC) (note: this comment was edited by its authour AFTER it was replied to)

sorry but that doesn't make sense. reactive power is just a quirk of the way electrical cuircuits work it doesn't represent ANY net transmission of power. Indeed in a balaced 3-phase system it doesn't even represent any instantanious trasfer of power. so if the power flowing into the generator really is equal to the apparent power then the generator would make insane amounts of heat with low power factor loads. do you have any sources for the claim you just made?! Plugwash 03:40, 24 Jun 2005 (UTC)

No, it is more than a quirk of the way electrical circuits work. Though *ideally* it does not represent any net transmission of power, in practice it does. Unfortunately, if you look at the magnitude of Z of a material through which the power is conveyed or used, you will find that there is resistance (ac) at the oscillation frequency. Though experiment: take a ring of copper. Induce a current in it. The current wave will die out overtime. Repeat with a superconductor: you can store energy for a very long period of time. So it goes with reactive power. Pushing the reactive power back and forth along the conductor induces losses. Thus, as the power factor degrades, you must size up all your components... the amounts of your active materials and your dielectrics on the basis of S. The joule loss of an m-phase balanced system is given by dP = m*r*(S/V)^2 where V is the line-neutral voltage, S is the apparent power, and r is the magnitude of Z.

"Every elementary nonactive component of S has two basic attributes:

• It causes power loss in the system
• It is the amplitude of an oscillation of power which does not contribute to a continuous unidirectional transfer of energy" (Emanuel, A., "On the Definition of Power Factor and Apparent Power in Unbalanced Polyphase Circuits with Sinusoidal Voltage and Currents" IEEE Transactions on Power Delivery, Vol 8., No. 3, July 1993

"The hottest spot temperature in transforms, alternators and cables is a function of [the Apparent Power]" (ibid)

So, the load seen by the generator depends on not only the energy transferred but on the energy losses from both the energy transfer and the oscillation. --Pearlg 23:07, 24 Jun 2005 (UTC)

---

The concepts of reactive and apparent power may be extended to multi-phase systems by summing up the apparent powers of the individual phases. It should however be noted that in an unbalanced multi-phase system the overall apparent power may be higher than ${\sqrt {P^{2}+Q^{2}}}$ where P and Q are the total real and reactive powers. -- I'd like a cite for this.

The total VA is the sum of the VA figures for each phase, with the voltage taken between line and neutral. Historikeren (talk) 17:19, 14 November 2014 (UTC)

Apparent power is used to describe the power load as seen by a generating source. It is the vector sum of the real power, which represents energy transferred from the source to the load, and reactive power, which represents energy that circulates between the source and the inductive and capacitive energy storage elements of the load. It is typically of most interest in power transmission and distribution. $|S|^{2}=P^{2}+Q^{2}$

move later to better spot complex power is a complex quantity which captures information about both the magnitude and type of power consumed by a load. It can be defined as the product of the phasor representation of rms voltage and the complex conjugate of the phasor representation of current. Real power is the real part of complex power, reactive power is the imaginary part of complex power and Apparent power is the magnitude of complex power. $S=P+jQ$

All the math for calculating Watts, VARs, and VA, assumes that the voltage and current waveforms are purly sinusoidal. If any harmonic content is present, these calculation produce incorrect results. 173.165.52.29 (talk) 20:53, 17 January 2012 (UTC)

Who coined the misleading and incorrect term 'Apparent Power'? The power is the power, it needs no adjectives. If a term is needed for active power, name is what it is, the average power. Volts, amps and power are understood, VA is unambiguous; but power qualified by an obscure adjective confuses people who suspect quite correctly that adjectives usually mislead. Historikeren (talk) 17:19, 14 November 2014 (UTC)

---

"At every instant the product of voltage and current is positive or zero, the result being that the direction of energy flow does not reverse." What is this trying to say? It isn't a correct sentence; it's just two dependent clauses stuck together with a comma. It's missing the part, between the two clauses, that can stand alone as a sentence. For example: "At every instant...", [something happens], "the result being that...".Pbyhistorian (talk) 20:07, 28 April 2020 (UTC)

Reactive Power

Looking carefully you will see that the sign reversal of the product of V and I occurs every quarter cycle, not every half cycle. I had to draw it out because the 90 degrees does not allow for that to occur for a half cycle and it choked my senses, so I drew it out. Yes, I know that adds up to a half cycle per cycle, but when getting down to that level it is obvious that the sign of V and I are opposite on alternate quarter cycles.... Regards, -- Steve -- (talk) 01:23, 16 January 2017 (UTC)

Notation

"(In this section overline will be used to indicate phasor or complex quantities and letters with no annotation will be considered the magnitude of those quantities.)"

Is this a standard notation? - Omegatron 23:16, August 14, 2005 (UTC)

well its what my university lecturers use i dunno if its a standard beyond that though. Plugwash 23:19, 14 August 2005 (UTC)

It wasn't standard when I was studying or practising electrical engineering (although that may just indicate how old I am!). A one-side-head horizontal arrow over a symbol was sometimes used to indicate a vector quantity, but most texts used boldface symbols for that. I always used a simple overline in the statistics sense - a mean or average (rms of course). Magnitude was denoted with matrix notation e.g. |z|. Plain symbols were used only for DC. Of course we used e for electromotive force and i for current, which drove the mathematicians nuts because they had totally different meanings for them. To top it off, because i was already in use, we used j for what mathematicians call i. I'm certain we can never find a notation that satisfies everyone, so we have to clearly specify the one that we use, then keep it consistent across related articles. Boldface and || have the advantage that they can be expressed directly within WP - no CSS or PNG required. JohnSankey 17:54, 5 October 2005 (UTC)

That's standard enough. As long as we clarify in an article whether:

• V = phasor, |V| = magnitude ([1] [2] [3])
• V = magnitude, ${\overline {V}}$ = phasor

Actually, it seems the only uses of overline are WP mirrors... :-\ Including complex number, which uses overline to mean complex conjugate. - Omegatron 01:01, August 15, 2005 (UTC)

I suspect that the use of overline for phasors is borrowed from some kind of vector notation (after all you could consider a phasor to be a two dimensional vector rather than a complex number its just easier to do the required calculations with it treated as a complex number). As for overline not being used much on the web i suspect that is a case of simply noone knowing that its availible (its only availible through CSS not through the old style html tags). Plugwash 00:11, 25 August 2005 (UTC)

In the article are these three sentences:

If the load is purely reactive, then the voltage and current are 90 degrees out of phase and there is no net power flow. This energy flowing backwards and forwards is known as reactive power. A practical load will have resistive, inductive, and capacitive parts, and so both real and reactive power will flow to the load.

The first sentence states: If the load is purely reactive... there is no net power flow.

The third sentence seems to contradict: [... both real and] reactive power will flow to the load. As reactive power has no net flow, it is confusing to include reactive power when writing of a flow to the load. Alexander 420 (talk) 22:13, 23 March 2009 (UTC)

Math markup

I try and avoid png rendered math inside text because it looks so ugly inline. What do others think? Plugwash 23:22, 14 August 2005 (UTC)

Hehehehee. Are you sure you want to ask that? Wikipedia_talk:WikiProject_Mathematics/Archive4(TeX) I really don't think we should be using CSS for overlines, though, as it's not necessarily supported by all browsers.

Proposed mergers

Right now, the merges suggested look like this (i think):

Electric reactance -> AC power -> Alternating current

I'm okay with this, except may I suggest that we first merge Electric reactance -> Reactance, so that the mergers would look like this:

Electric reactance -> Reactance -> AC power -> Alternating current

Reactance appears to this layman as the better written article. The only reason for merging Reactance -> Electric reactance, is to distinguish this from the sense in which Reactance is used in chemistry. Just a thought. Vonkje 11:51, 3 October 2005 (UTC)

I consider the concepts of electrical current/voltage, resistance/reactance and power to be sufficiently different that they should not be merged, otherwise the combined article will become too long and very difficult to organize clearly. I note that there is inadequate discussion in these articles of non-sinusoidal waveforms, particularly of the substantial 3rd and 5th harmonics generated by the non-linearity of standard power transformers - that would make a combined article even longer. Then there are the square and 2-step waveforms of DC-AC power converters. I recommend keeping these three separate but consistent, with appropriate cross links. As a retired electrical engineer, I could try to start this process, but would do so only when agreement is reached on separation or merger. JohnSankey 15:31, 5 October 2005 (UTC)

I do not think it is a good idea to merge electric reactance with AC power. The concept of reactance is important in other areas of electrical engineering, such as RF circuit design. Merging would change its apparent position from a fundamental concept in EE to an apparent subtopic of power transmission. Future articles that refer to reactance would become extremely awkward. Mbset 07:23, 15 October 2005 (UTC)

Can we remove some of the merge templates then?

Watts, volt-amps, and power meters

This is a very nice article, but a bit more than I need to know. I'm trying to understand, something more basic, the difference between Watts and Volt-amps in the real world. I have a meter that measures both watts and VA when you plug in normal household appliances. If I plug in an incandescant bulb the watts and VA are virtually identical, if it is a compact flourescant bulb the VA are almost twice the watts. I understand why this is, but my question is more basic. Which is being measured by my electric meter? I'm under the impression that it counts VA hours but calls them watts. If this is so, why do all electric appliances come rated in watts and not VA? -- Samuel Wantman 06:35, 18 January 2006 (UTC)

I think at least here in the uk domestic meters do actually measure watts (meters for large commercial and industrial installs measure watts and VArs seperately). but i'm not entirely positive. Plugwash 14:16, 18 January 2006 (UTC)

VA hours would not be equivalent to watts. It's equivalent to joules. The difference between VA and W is real vs apparent power, as explained in the article. — Omegatron 17:20, 18 January 2006 (UTC)

Reactive Power

Reactive Power carries much more significance than what is highlighted in this article. I think that Reactive Power should not be combined with AC Power. A few major points about Reactive Power not discussed here, are:

1. Reactive Power - Power System Voltage regulation (Voltage Control)
2. Significance of Reactive Power in Power Industry today
3. Efforts on part of Regulatory/Governing bodies to ensure availability of reactive power for System Stability
4. Compensation of Electric Generators for providing Reactive Power in emergency situations

Other discussions will come up as soon as we open this topic. Therefore, I request you to create a separate topic for Reactive Power.

It certainly deserves mention in a general article on AC power but there is no reason there cannot be a seperate article on it if you belive you can produce enough content for one. Plugwash 21:25, 17 November 2006 (UTC)

I concur with the request to create a separate and detailed topic for "Reactive Power". The search on this phrase led me to this article, which was a good basic review (I am an MSEE and have recently returned to the Power field several decades after having studied it in college.) I specifically care about the four sub-topics related to Reactive Power as outlined above. RWVesel 16:31, 11 July 2007 (UTC)

Included a paragraph that explained how utilities work, and whether or not they charge for reactive power. Also introduced the idea of power factor. Nisha123456789 (talk) 19:14, 9 December 2015 (UTC)

Terminology

This entire article is inconsistant with standard terminology employed by electrical engineers. We speak of Volts, Amperes, and Watts, noting the differences between peak power (Watts) and root mean square power (Watts). This article doesn't mention any of these. Celestialmechanic 16:10, 11 August 2007 (UTC)

This is pretty normal terminology in the electric power industry. It knocked me for a spin when I started working in the industry 20 years ago, and took me a while to get up to speed. It seems to be more common these days: for example you'll find VA being used in preference to Watts (even though the units and magnitude are the same) on quite small UPSes these days. Resuna (talk) 23:34, 16 June 2008 (UTC)

Different power types are expressed in different units to not confuse them, although all of those units are dimensionally the same (W = J/s = VAr = VA.)

The standard is: Active power and instantaneous power are measured in watts, reactive power is measured in volt-amperes reactive, apparent power and complex power are measured in volt-amperes.

In sinusoidal steady state, instantaneous power can be decomposed into two components: instantanoeus active power and instantaneous reactive power. The the peak value of the former is 2·P (where P is active power or average power) and the peak of the latter is |Q| (the absolute value of reactive power.)

What do you mean with peak watts and RMS watts? What is described in this other article? At least in power systems, I've never heard of peak and RMS watts. --Alej27 (talk) 01:48, 21 October 2020 (UTC)

ac power

dear sir how power(reactive/real )is scalar quantity while both are directional.thanks. —Preceding unsigned comment added by 119.73.111.178 (talk) 22:56, 10 February 2009 (UTC)

Reactive power and real power are always 90 degrees apart. In terms of linear algebra they form basis vectors of a two-dimensional complex space. The volt-amps are the vector sum of the Wh (real) and VARh (reactive) power. So, only volt-amps have a changing direction in the space. The power factor is actually the cosine of the "voltage to current angle." I.e., Wh/VAh Hope that helps. Ray Van De Walker 01:07, 7 March 2010 (UTC)

How is active power and reactive power scalars when they have direction? Good question. That's the same as asking why current is also a scalar when it has direction.

Well, in the case of current, I see it in the following way. Consider a circuit diagram consisting of a voltage source connected in series (or in parallel) with a resistor. The circuit diagram is drawn like this: a vertical voltage source to the left, a verticasl resistor to the right, a horizontal wire on the top connecting the voltage source and resistor, and a horizontal wire on the bottom. Now, in one side of the resistor, draw a tiny arrow that points down. This arrows tells which direction will be considered positive for the current, and is known as reference direction. After you apply Ohm's law you get a mathematical expression for the current. This value is the same for all of the currents in each cross-sectional area of the wires of this circuit, because it is a series connection and so the current through each device is the same.

This seems good, so it suggests to use scalars. But it doesn't answer why not use vectors instead? To answer that, first you could remember how working with vectors is more tedious than with scalars. Secondly and more important, there's no single vector that would describe the spatial direction of current in each segment of the circuit. For example in the resistor the vector would have to point down, but in the source it would have to point up; since a vector doesn't have two directions but only one, we would need to write the second vector with a different symbol. In other words, if we used vectors, the current in series connection would need to be written with different symbols depending on the spatial direction of current; this would be tedious.

A third and important way to see why treating current as a scalar is fine, is to think about what does its direction mean. When you see the waveform of a sinusoidal wave, you see negative and positive values. This means that on the positive values, positive electric charge is flowing in the reference direction; on the negative values, positive charge is flowing in the opposite direction. Et voilà! There's no need to use vectors, since the sign of current already tells us the direction of flow of charge!

By the way, in the case of LTI AC circuits we usually work with complex numbers, which are very similar to two-dimensional real vector (except the former has dvision as a defined mathematical operation.)

Okay, so now you should know why we use scalars and not vectors for current. What about active and reactive power? Well, let's go back once again to what their directions mean. In the case of active power, remember active power is a synonym of average power. Thus, the direction of average power indicates which is the average direction in which energy is flowing. For example, in a resistor, if you use the passive sign convention, a positive average power means energy that's flowing from source to resistor. In an inductor, its average power or active power is zero, meaning energy on average doesn't flow to either direction (which is true.) My point is, once again, the sign of active power already tells the direction of flow of energy, so there's no need to treat it as a vector. In the case of reactive power, a somewhat similar explanation applies.--Alej27 (talk) 02:26, 21 October 2020 (UTC)

Unbalanced Polyphase Systems

Could someone talk about the resolution that came about in the 1990s? That is an interesting story and should be further discussed in this article, or a link should be provided if it is discussed elsewhere. —Preceding unsigned comment added by 131.183.23.25 (talk) 15:39, 4 September 2009 (UTC)

Dubious

"Power is defined as the rate of flow of energy past a given point."? Goes against what I have beent taught/learned and read before. (Are they confusing energy and current where flow 'past a given point' is correct?)
However in Power (physics) it says "In physics, power is the rate at which work is performed or energy is converted" which seems much more correct. Especially 'work is performed' not just 'rate of flow of energy'. --220.101.28.25 (talk) 02:25, 26 November 2009 (UTC)

Did you read the article? The reason this is the case is because not all power in an eletrical system does work. Real Power does work, but Reactive Power does not. It is a transfer of energy to one place, and then back from whence it came, with no work done in between, besides heating up the physical elements (losses). Reactive power exists because all inductive and capacitive elements in a electrical system cause such "net zero" energy flows to occur. —Preceding unsigned comment added by 96.231.76.6 (talk) 05:41, 29 January 2010 (UTC)

Instananeous power can be defined either as the rate at which work is done (the second definition you used), or as the rate at which energy is traferred (basically the first defintion you used.) Both definitions are correct.

Some people might say this is wrong because, from the thermodynamics point of view, not all energy is work (for example, heat is also another form of transfer of energy.) But at least in electrical engineering we consider both definitions equivalent.

Regarding the reply the person above me said, just to make it clear, we shall distinguish between instantaneous work and net work. Both resistors and reactor (inductors and capacitors) perform instantaneous work, but only the former perform net work (i.e. the net work done by inductors and capacitors is zero.) --Alej27 (talk) 03:08, 21 October 2020 (UTC)

Clarification Needed

This seems like complete rubbish to me, "In alternating current circuits, energy storage elements such as inductance and capacitance may result in periodic reversals of the direction of energy flow.
If it's an AC circuit it's reversing anyway isnt it? Are they talking about inductance and capacitance in the power lines, causing unintended reversals that interfere with the normal AC, for example? --220.101.28.25 (talk) 02:50, 26 November 2009 (UTC)

Nope. Energy, not current. AC through a resistor has unidirectional power flow. AC to a reactive load has points where the power flow reverses on each cycle. --03:00, 26 November 2009 (UTC)

Agree w/ second poster. If you have a purely resistive load in an AC circuit, all of the energy is being dumped into the load (one direction of energy flow), regardless of the fact that the current is alternating directions. On the other hand, if you have a capacitive or inductive element, energy gets stored in the element, and then returns to the source, hence reactive power. —Preceding unsigned comment added by 96.231.76.6 (talk) 05:48, 29 January 2010 (UTC)

The two people above me are correct. In a resistor, energy flow is unidirectional. In an inductor or capacitor, energy flow is bidirectional.

It's important to distinguish between the two types of flow in circuits: flow of charge (i.e. current) and flow of energy (i.e. power). The question of the first person is the result of confusing these two flows (I'm not blaming them, though; electromagnetism is quite counterintuitive.)

I suggest watching this video (https:// youtu. be/agujzHdvtjc) from Eugene Khutoryansky on transformers to clarify the asked question. In that video, charges are represented as red and pink points (so, the flow of these points is current.) Energy is represented as boxes. Throughout the video, Eugene assumed a purely resistive load (although he didn't say it explicitly.) At the minute 1:30, you can see that, while charge flow is alternating, energy flow isn't; it's always going from source to (purely resistive) load.

As a side note, since we're talking about the direction of these two flows, it's also important to talk about their speed: charges move at drift speed which is very low, while energy moves at the speed of light. --Alej27 (talk) 03:16, 21 October 2020 (UTC)

Terminology

"The portion of power flow that, averaged over a complete cycle of the AC waveform, results in net transfer of energy in one direction is known as real power. The portion of power flow due to stored energy, which returns to the source in each cycle, is known as reactive power."

This terminology is wrong. Power cannot be power flow. Power is energy flow (Watts, energy / time). I don't even know what "power flow" would mean, perhaps the time rate of change of power. —Preceding unsigned comment added by 96.231.76.6 (talk) 05:43, 29 January 2010 (UTC)

I agree with the person above me.

Charge flow is current, yet people/electrical engineers use the phrase "current flow." This phrase is redundant because current is already a flow. Now, some people might say I'm acting dumb or I'm being too strict, but in science/engineering we shall be strict with the words! To support my point, below I quote a text from section 17.1 of the book College Physics, volume II by Raymond Serway et al. (p. 571):

"The phrases flow of current and current flow are commonly used, but here the word flow'- is redundant because current is already defined as a flow (of charge). Avoid this construnction!"

Similarly, energy flow is power, so saying "power flow" is redundant. I'm aware that in electric power engineering, there's a type of study known as power flow, but its name is redundant.

Maybe the reason why engineers use the phrase current flow and power flow is because current and power are terms more commonly used than charge and energy. Or maybe they don't even pay attention. --Alej27 (talk) 04:30, 21 October 2020 (UTC)

am I going to open a can of worms?

I've read the article and all the comments on this talk page and everything / everyone seems to be describing a full sinusoidal wave form but what about North America where 220-240vac sine wave gets split into two 110-120vac half sine waves?

for examle the picture of the blinking light trace describes 2 blinks per wave whereas in north america if the light was connected to 110-120 ac wouldn't there be just 1 blink per wave?

in general, I've been finding wiki articles regarding mains power lacking not adequately describing (or ignoring) North American household use of AC

I'm not an effective writer so I'm not qualified to offer anything more than a suggestion or a request that someone modify these articles to include single phase half-wave power usage :-) — Preceding unsigned comment added by 24.6.92.12 (talk) 05:49, 25 February 2012 (UTC)

<months later> Have a look at Split-phase electric power. It's not "two half sine waves". --Wtshymanski (talk) 13:29, 15 May 2012 (UTC)

Average power

«This method of calculating the average power gives the real power regardless of harmonic content of the waveform. In practical applications, this would be done in the digital domain, where the calculation becomes trivial when compared to the use of rms and phase to determine real power.

$P_{avg}={\frac {1}{T}}*\sum _{k=1}^{n}v[k]*i[k]$»

Shouldn't it be: $P_{avg}={\frac {1}{n}}*\sum _{k=1}^{n}v[k]*i[k]$ ?

89.181.225.20 (talk) 01:11, 15 May 2012 (UTC)

Complex power

The diagram is nice, but WHAT is the formula, or a precise definition of complex power? It is not stated anywhere in the article... --82.54.173.32 (talk) 20:53, 6 June 2012 (UTC)

Complex power is defined ("defined" means you can't prove it from any other equation or theorem) as one half the voltage phasor times the complex conjugate of the current phasor, or, as the RMS voltage phasor times the complex conjugate of RMS current phasor. Why? Because this leads to a very useful quantity: its real part is the average or active power, its imaginary part is the reactive power, its magnitude is the apparent power, and it's angle is the power factor angle.-- Alej27 (talk) 04:40, 21 October 2020 (UTC)

Wrong HTML Anchor

In the contents navigator, clicking on "Reactive power" leads to "1 Active, reactive, and apparent power". Shouldn't it lead to "3 Reactive power"? 129.247.247.238 (talk) 10:27, 18 February 2015 (UTC)

Reorganization of Reactive Power Section

I have edited the reactive power section to clarify the differences between inductive loads and capacitive loads and their effects on reactive power and power factor. Some statements were made in the form of "this causes the voltage to lag the current" and I changed them to reflect the convention that voltage is defined as 0 degrees. I also added more information about sourcing vs. sinking reactive power and added the fact that inductive loads are primarily made up of generators and motors. A more in depth discussion about why reactive power is useful or necessary for power system operation.

Regarding the reactive power control section, I looked around and couldn't find the formula that was referenced. Also the phrase "pre-fault reactive generator use" is confusing, and I'm not sure what it means.

A figure illustrating the relationship between complex power and voltage and current and their shared angle would also be illustrative and useful. — Preceding unsigned comment added by Tripleripple (talk • contribs) 07:30, 29 April 2015 (UTC)

Section: Capacitive vs. Reactive Loads

It says, "This voltage increases until some maximum dictated by the capacitor structure." There are other things that also affect the maximum voltage a capacitor will charge up to, such as other circuit elements, so the point of that sentence isn't clear, not in context or otherwise. I think the explanation of the current leading in a capacitor might be more concise if that sentence were simply eliminated. I might put more emphasis on the voltage of a capacitor being unable to change instantaneously (with an explanation of why can't it -- in the cases of increasing or decreasing applied voltage), thereby causing a phase lag in the voltage relative to current when the applied voltage changes, i.e. voltage-lagging in the capacitor (or current leading).

75.110.98.103 (talk) 15:52, 10 March 2016 (UTC)

I agree with you. Since the current through an inductor can't change abruptly but voltage can, current lags voltage here. Since the voltage across a capacitor can't change abruply but current can, voltage lags current (or also current leads voltage) here. This is the explanation of the phrase ELI the ICE man. --Alej27 (talk) 04:48, 21 October 2020 (UTC)

Comments - I am trying to understand this

Text says:

This method of calculating the average power gives the active power regardless of harmonic content of the waveform. In practical applications, this would be done in the digital domain, where the calculation becomes trivial when compared to the use of rms and phase to determine active power.

$P_{\text{avg}}={\frac {1}{n}}\sum _{k=1}^{n}V[k]I[k]$

The link between the equation and the preceding text isn't clear. Is it meant that P(avg) = P(rms)? What is the term k? Is it just an arbitary small increment or is it an increment of time (in reallity)? It isn't defined -just saying. Cinderella157 (talk) 10:20, 15 March 2017 (UTC)

more

: $pf={P_{a}+P_{b}+P_{c} \over |S_{a}|+|S_{b}|+|S_{c}|}$

that is, the quotient of the sums of the active powers for each phase over the sum of the apparent power for each phase.

$pf={P_{a}+P_{b}+P_{c} \over |P_{a}+P_{b}+P_{c}+j(Q_{a}+Q_{b}+Q_{c})|}$

Is that: "over the sum of the absolute values of the apparent power for each phase"? I had to think what those bars meant (it was a long time ago). Cinderella157 (talk) 10:26, 15 March 2017 (UTC)

more

product terms in more detail we come to a very interesting result.

${\begin{aligned}&A\cos(\omega _{1}t+k_{1})\cos(\omega _{2}t+k_{2})\\={}&{\frac {A}{2}}\cos \left[\left(\omega _{1}t+k_{1}\right)+\left(\omega _{2}t+k_{2}\right)\right]+{\frac {A}{2}}\cos \left[\left(\omega _{1}t+k_{1}\right)-\left(\omega _{2}t+k_{2}\right)\right]\\={}&{\frac {A}{2}}\cos \left[\left(\omega _{1}+\omega _{2}\right)t+k_{1}+k_{2}\right]+{\frac {A}{2}}\cos \left[\left(\omega _{1}-\omega _{2}\right)t+k_{1}-k_{2}\right]\end{aligned}}$

A, omega (and k) are not defined? Cinderella157 (talk) 10:31, 15 March 2017 (UTC)

Which omega is zero - w1 or w2? Cinderella157 (talk) 10:34, 15 March 2017 (UTC)

Cinders,

Some comments:

Be careful with your terminology. There is no such (useful) thing as "RMS Power". RMS only refers to voltage and current values. The RMS (Root Mean Square) values of Voltage and Current are the effective values. This means they are the values that have the same effect as a DC quantity of that value for calculating (average) power. A voltage of x volts RMS give the same power in a circuit as x volts of DC would. Therefore, P(avg) = V(RMS) * I(RMS)

Average power is pretty much what you think. It is the power over a relatively long term.

In the US, the term "power" means "average power". This is the power averaged over (at least) one full cycle of the AC waveform. This term is used to distinguish it from instantaneous power or the power V*I at one single instant. The term "active power" is not used in any context I have ever been involved in.

The formula you question is a discreet step version of the integral formula just above it. The integral version uses the continuous integral of the voltage and current to calculate (average) power. The discreet formula is saying that you sum the instantaneous power at small time increments (k) over some total time (n). The term 'k' signifies the voltage and current values at the times 'k' as 'k' is stepped from time 1 through 'n'. I think it would have been better to use 't' instead of 'k' to indicate time steps here.

In the "Multiple frequency systems "cos" formulas, "A" is the amplitude (cos has a peak value of 1), omega is the frequency in radians per second, and 'k' is the phase offset of that component frequency. These are standard notations for sinusoidal signals.

I'd have to go back to school to address the Omega1, omega2 question. The first equation is expanded using a trig identiry that is lost to memory... I'm not sure just what that trig identity is doing, nor just what your question is asking. Sorry.

The vertical bars mean absolute value. I believe (but could be wrong) those are there because for reactive circuits there are some instantaneous power values that go negative due to the phase shift between voltage and current waveforms. That is, the voltage is positive when the current is still flowing in the opposite direction and visa-versa. In other words you have V*(-I) or (-V)*I. In a purely resistive circuit V and I are always in phase and therefore have the same polarity.

Regards -- Steve -- (talk) 05:42, 16 March 2017 (UTC)

@ -- Steve -- , Thanks for the reply. I realise once you said it that P(rms) is meaningless - I was meaning P calculated from the rms values of V and I ? I was using P(rms) to mean a value calculated this way rather than one derived by summation. I guess, with the cos function, it is using terms that aren't definded (as it does in the sum compared to the integral). In part, I was pointing out some things that weren't clear (to me), hoping that somebody could clarify the text. Cinderella157 (talk) 11:33, 16 March 2017 (UTC)

I don't think the vertical bars refer strictly to the absolute value of apparent power, but instead the magnitude of complex power. Apparent power is always positive, since Vrms and Irms are both positive (unless a convention is used, though I have never heard of one nor seen negative apparent power.) Alej27 (talk) 23:20, 22 October 2020 (UTC)

Asterisk

Please explain asterisk in formula. —DIV (120.17.54.174 (talk) 12:33, 5 August 2018 (UTC))

It stands for the complex conjugate of the complex number right before the asterisk. In the Complex power equation, it stands for the complex conjugate of the current phasor. --Alej27 (talk) 04:53, 21 October 2020 (UTC)

Is it okay for you if in the first paragraph I change "power" to "instantaneous power"?

The term "power" has a lot of meanings. If we're talking about transformers, it usually means the apparent power. If we're talking about motors, it usually means the output mechanical power. If we're talking about a load, it usually means the active power (also known as average power or real power.) If we're talking about a capacitor bank, it usually means the reactive power.

So, as you can see saying "power" alone might be misleading. Because of this, I suggest to change in the very first paragraph of this article, the word "power" for "instantaneous power", which is what whoever wrote it meant (the rate of transfer of energy or the rate of work being done.) --Alej27 (talk) 01:21, 21 October 2020 (UTC)

What's the point of the section "Unbalanced polyphase systems"?

In that section, it reads "While active power and reactive power are well defined in any system, the definition of apparent power for unbalanced polyphase systems is considered to be one of the most controversial topics in power engineering." Why is it controversial? In a two-terminal (i.e. single-phase) element/device/load/generator, apparent power is defined as the product of RMS voltage times RMS current. This definition applies whether in sinusoidal steady-state (no harmonics) or in non-sinusoidal steady-state (with harmonics), and whether in balanced or unbalanced systems.

In balanced three-phase systems, the previous definition is usually called single-phase apparent power or per-phase apparent power, while the three-phase apparent power or total apparent power is three times the previous quantity.

In unbalanced three-phase systems, the single-phase apparent power is still RMS voltage times RMS current.

Maybe the controversy the section talks about is regarding three-phase (and not single-phase) apparent power in unbalanced three-phase systems? Can someone clarify me this? If that's true, then my point of view is that people/engineers can't expect apparent power to be the sum of the single-phase apparent power of each leg of the device, not because the system is unbalanced, but because the apparent power is not a conserved quantity (unlike active/real power, reactive/quadrature power, and complex power). --Alej27 (talk) 01:03, 31 October 2020 (UTC)

Reason for reverting article?

The user @Wtshymanski: removed my edit of the article and change it to this version. They also reverted the talk page, from this version to this version.

Their reason: "a textbook treatment is not appropriate for an encyclopedia article; revert to earlier version"

My questions: what is meant by "a textbook treatment"? Does Wikipedia have an article in which they say "a textbook treatment is not appropriate for an encyclopedia article"? If so, please share it. I found this, on items 6 and 7. In my edit of the article, I didn't prove any of the equations. I posted the final result. Also, I added a lot of references throughout the texts. So please justify. Please explain in which way I should've redacted, so that it is appropriate for an encyclopedia article.

It's true there were some statements in the article in which I didn't use a textbook reference, and instead I used a reference to the talk page where I proved the statement, and that may be considered as "new theory", so it should be removed according to item 1 of this page from Wikipedia. For examples, some formulas in the section Measurement and in the subsection Net energy in AC steady-state. So they should be removed. That was my mistake. But only those statements should be deleted, not absolutely everything I wrote/fixed, I think.

In my edit of the article, I also clarified some texts. A random person reading the article may think the formulas posted in the current version are valid for any AC circuit, which is wrong. It is never stated they're valid for sinusoidal steady-state (without harmonics), not for non-sinusoidal steady-state (with harmonics) or in transient state. What's the problem of being specific/clear?

I don't think you even read the section Measurement (I apologize if you indeed did). It had barely any text and formulas, but it had references, and people could've understood it. Please explain why that section had "a textbook treatment". A textbook would've proven those formulas, for example; in my edit, the formulas weren't proven, only the final formula was shown, and also images to clarify.

I had also changed the second lead paragraph of the article. But you didn't keep it. What was the problem there? I had just made it more specific.

Why didn't you also delete the sections Reactive power, Reactive power control, Power factor, and Calculations and equations? They don't have any references. And Wikipedia is about verifiable facts/reliable sources.

Have you read the article about derivatives? They actually derived the formula. That is a textbook treatment. Why don't you delete that? In the article on nodal analysis they even showed examples; textbooks use examples, so why don't you delete those examples? And what about the article on delta-wye transformations? They have a section demonstrating the formulas, which is what textbooks do, which is against what you said, so you should remove that too. The article on electric power, on section Explanation, doesn't cite any references, so why isn't that also deleted?

I think instead of deleting all my work, you could've improved it. Please tell how I should've written my edit. Thanks in advance.

--Alej27 (talk) 04:50, 13 June 2021 (UTC)

I recommend the essay Wikipedia:What Wikipedia is not, especially the section "Wikipedia is not a manual, guidebook, textbook, or scientific journal". An encyclopedia is supposed to give a concise general overview of a subject for a reader not specialized in the topic. It is not meant to teach a subject from first principles. Extensive derivations are undue detail for an encyclopedia article; it is sufficient to refer a statement to an authoritative reference which is free to go int more detail. Summary, overview, general reader - if you fill an article with calculus, only the calculus students will read it and a general reader will be frustrated. Give this basis, there was no proper way to shorten your treatment as it was proceeding as if it were written for a tutorial, not as a general overview. Wikipedia is not reliable, but it is verifiable, as you correctly observe. --Wtshymanski (talk) 04:41, 14 June 2021 (UTC)

@Wtshymanski: Thanks for replying.

"It is not meant to teach a subject from first principles." // My edit didn't teach the formulas from first principles. It showed the final formulas. And if you read the section "Calculations and equations" of the current version, you'll see it also shows just the formulas. So why don't you delete that too? If you don't explain why not, I'll delete it, because it also shows formulas, just like my edit.

"Extensive derivations are undue detail for an encyclopedia article; it is sufficient to refer a statement to an authoritative reference which is free to go int more detail." // That's exactly what in did in the statements in which I used a textbook for reference: I didn't show any derivation, I showed the final formulas and added a textbook reference (i.e. an authoritative reference). So why did you delete it?

"Give this basis, there was no proper way to shorten your treatment as it was proceeding as if it were written for a tutorial, not as a general overview." // Why is it needed to shorten it? There's no limit in an article's length, is it?

"Wikipedia is not reliable, but it is verifiable, as you correctly observe." // The sections "Reactive power", "Reactive power control", "Power factor", and "Calculations and equations" of the current version of the article don't have any references, so why aren't those sections deleted?

Please read this article and head to the section "Compressible flow". Note there are a bunch of equations, similar to my edit. Someone without knowledge of calculus won't understand them. So that should also be deleted, right? Furthermore, this article and this article are literally math-only, so why don't you delete those articles?

--Alej27 (talk) 05:15, 14 June 2021 (UTC)

Articles are often too long. I recommend the guideline at Wikipedia:Article size. A wall of maths is never a good plan in an encyclopedia article. --Wtshymanski (talk) 23:07, 14 June 2021 (UTC)

Also see WP:OTHERSTUFFEXISTS. Just because one article is in error, it is not a justification to create another one. 86.129.19.88 (talk) 12:28, 15 June 2021 (UTC)

Let's find a new lede image

The image in the lede is awful. It's uninformative eye candy. Stare at it long enough and you'll work out how it's related to AC power, but what's wanted for the lede is an image that unambiguously and immediately says "AC power": "[T]he image used should be relevant... It is also common for the lead image to be representative because it provides a visual association for the topic, and allow readers to quickly assess if they have arrived at the right page," per MOS:LEADELEMENTS. You shouldn't have to work backward from a knowledge of the topic to deduce how in the world the lede photo introduces it. Yappy2bhere (talk) 22:50, 11 August 2021 (UTC)

So what image comes to your mind when you think of AC power? And if you say a pointer on a scale of a wattmeter, I will be weeping softly at my keyboard. It's an abstract expression, it has no visualization, and if the hapless reader is confused by the picture, she'll just have to read all that boring text to figure out what the topic is. Thank goodness we explained a hundred times about RMS values. Can anyone tell the pictures of Erskine Calder and Millard Filmore apart instantly, so that they know they've landed on the right article? --Wtshymanski (talk) 23:18, 11 August 2021 (UTC)

A while back I made some nonprofessional-looking images using GeoGebra, where I plotted the instantaneous voltage, instantaneous current, instantaneous active current, instantaneous reactive current, instantaneous power, instantaneous active power, and instantaneous reactive power waveforms, for lumped passive linear time-invariant two-terminal (i.e. single-phase) networks, driven by a sinusoidal voltage and operating in AC steady-state. The images also show the relation between apparent power, active power, reactive power, and the amplitude and time-mean of the instantaneous power, instantaneous active power and instantaneous reactive power. For a series RL load:

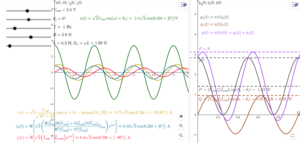
Figure 1. Click to amplify image.

For a series RC load:

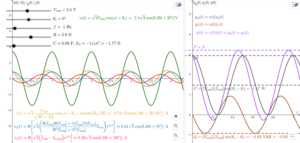
Figure 2. Click to amplify image.

Perhaps an image as the ones above might be helpful. For example, the article on Alternating current also has waveforms as lede images, despite electric current being a hard concept to visualize with bare eyes. --Alej27 (talk) 02:59, 12 August 2021 (UTC)

Clarify power factor example

The user Wtshymanski recently changed an example in the Power factor section of the article, to the following sentence:

"For instance, a power factor of 0.68 means that only 68 percent of the total current supplied (in magnitude) is actually doing work; the remaining 32% does no work."

I think it's misleading the phrase "the remaining 32% does no work". What does that 32% represent? Please clarify. As far as I know, there's no other 32%, because the relation between active current and reactive current is orthogonal, meaning $I_{\text{rms}}={\sqrt {I_{\text{rms,a}}^{2}+I_{\text{rms,r}}^{2}}}$, thus the reactive current is sin(arccos(0.68)) ≈ 0.73 = 73% the total current, not 32%, as shown in the following figure for a RL load.

Figure 1. Phasor diagram of phasor voltage, current, active current and reactive current for a RL single-phase load driven by sinusoidal voltage. Click to amplify.

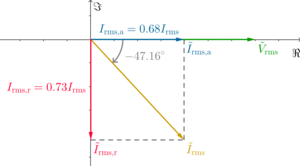
So, I think we should remove the phrase "the remaining 32% does no work". Or we could be more specific in the example, and instead say something like:

"For instance, in sinusoidal steady-state, a single-phase load with a power factor of 0.68 means that the RMS value of the active component of the total current (the one corresponding to the active power or net energy transfer) is just 68% of the RMS value of the total current".

or in fewer words:

"For instance, a single-phase load with a power factor of 0.68 means that the active current (the one corresponding to the active power or net energy transfer) is just 68% of the total current".

And if we want to talk about the remaining current, we could talk about the reactive current, adding the following to the previous sentence:

"On the other hand, reactive current (the one corresponding to the reactive power or no net energy transfer) is 73% of the total current."

What are your thoughts? --Alej27 (talk) 20:45, 12 August 2021 (UTC)